9131: ABC330 —— F - Minimize Bounding Square
[Creator : ]
Description
There are $N$ points labeled $1, 2, \dots, N$ on the $xy$\-plane. Point $i$ is located at coordinates $(X_i, Y_i)$.
You can perform the following operation between $0$ and $K$ times, inclusive.
- First, choose one of the $N$ points. Let $k$ be the selected point, and assume it is currently at $(x, y)$.
- Next, choose and execute one of the following four actions:
- Move point $k$ along the $x$\-axis by $+1$. The coordinates of point $k$ become $(x+1, y)$.
- Move point $k$ along the $x$\-axis by $-1$. The coordinates of point $k$ become $(x-1, y)$.
- Move point $k$ along the $y$\-axis by $+1$. The coordinates of point $k$ become $(x, y+1)$.
- Move point $k$ along the $y$\-axis by $-1$. The coordinates of point $k$ become $(x, y-1)$.
- It is allowed to have multiple points at the same coordinates. Note that the input may already have multiple points at the same coordinates.
After all your operations, draw one square that includes all the $N$ points inside or on the circumference, with each side parallel to the $x$\- or $y$\-axis.
Find the minimum possible value for the length of a side of this square. This value can be shown to be an integer since all points are always on lattice points.
In particular, if all points can be made to exist at the same coordinates, the answer is considered to be $0$.
You can perform the following operation between $0$ and $K$ times, inclusive.
- First, choose one of the $N$ points. Let $k$ be the selected point, and assume it is currently at $(x, y)$.
- Next, choose and execute one of the following four actions:
- Move point $k$ along the $x$\-axis by $+1$. The coordinates of point $k$ become $(x+1, y)$.
- Move point $k$ along the $x$\-axis by $-1$. The coordinates of point $k$ become $(x-1, y)$.
- Move point $k$ along the $y$\-axis by $+1$. The coordinates of point $k$ become $(x, y+1)$.
- Move point $k$ along the $y$\-axis by $-1$. The coordinates of point $k$ become $(x, y-1)$.
- It is allowed to have multiple points at the same coordinates. Note that the input may already have multiple points at the same coordinates.
After all your operations, draw one square that includes all the $N$ points inside or on the circumference, with each side parallel to the $x$\- or $y$\-axis.
Find the minimum possible value for the length of a side of this square. This value can be shown to be an integer since all points are always on lattice points.
In particular, if all points can be made to exist at the same coordinates, the answer is considered to be $0$.
Input
Input is given from Standard Input in the following format:
```
$N$ $K$
$X_1$ $Y_1$
$X_2$ $Y_2$
$\vdots$
$X_N$ $Y_N$
```
```
$N$ $K$
$X_1$ $Y_1$
$X_2$ $Y_2$
$\vdots$
$X_N$ $Y_N$
```
Output
Print the answer as an integer.
Constraints
- All input values are integers.
- $1 \le N \le 2 \times 10^5$
- $0 \le K \le 4 \times 10^{14}$
- $0 \le X_i, Y_i \le 10^9$
- $1 \le N \le 2 \times 10^5$
- $0 \le K \le 4 \times 10^{14}$
- $0 \le X_i, Y_i \le 10^9$
Sample 1 Input
6 5
2 0
5 2
0 3
3 2
3 4
1 5
Sample 1 Output
3
The figure below illustrates this case with the horizontal x-axis and the vertical y-axis.
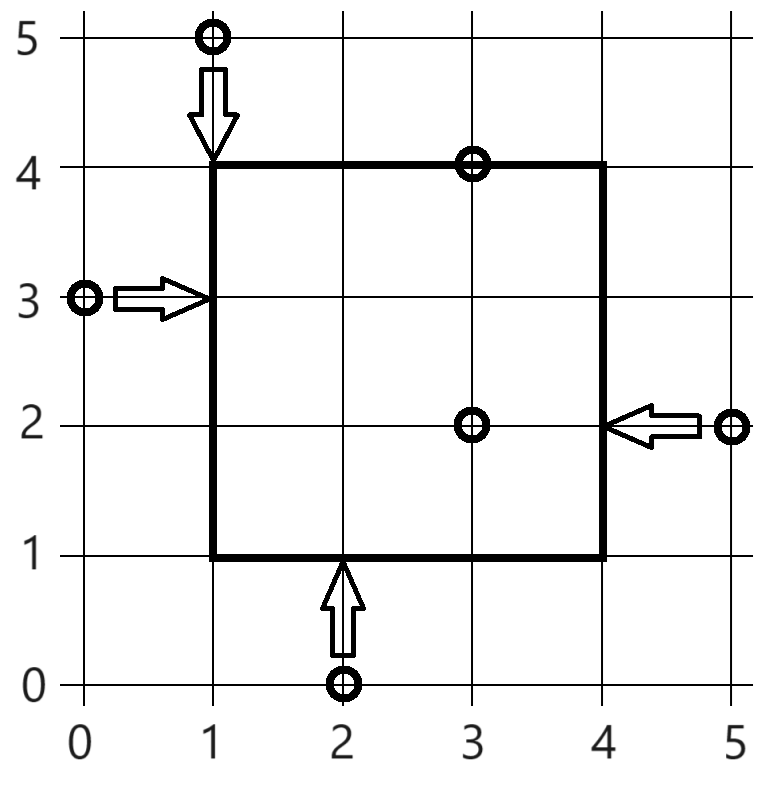
For example, after performing four moves following the arrows in the figure, you can include all points inside or on the circumference of the square shown in the figure with a side length of 33, and this can be shown to be the minimum value.

For example, after performing four moves following the arrows in the figure, you can include all points inside or on the circumference of the square shown in the figure with a side length of 33, and this can be shown to be the minimum value.
Sample 2 Input
4 400000000000000
1000000000 1000000000
1000000000 1000000000
1000000000 1000000000
1000000000 1000000000
Sample 2 Output
0
All points already exist at the same coordinates from the beginning.
For example, by performing zero operations, all points can be made to exist at the same coordinates, so the answer for this input is 0.
For example, by performing zero operations, all points can be made to exist at the same coordinates, so the answer for this input is 0.
Sample 3 Input
10 998244353
489733278 189351894
861289363 30208889
450668761 133103889
306319121 739571083
409648209 922270934
930832199 304946211
358683490 923133355
369972904 539399938
915030547 735320146
386219602 277971612
Sample 3 Output
484373824
HINT
相同题目:ABC330。