9123: ABC336 —— F - Rotation Puzzle
[Creator : ]
Description
There is a grid with $H$ rows and $W$ columns. Initially, each integer from $1$ to $(H \times W)$ is written exactly once in the grid.
Specifically, for $1 \leq i \leq H$ and $1 \leq j \leq W$, the cell at the $i$-th row from the top and the $j$-th column from the left contains $S_{i,j}$.
Below, let $(i,j)$ denote the cell at the $i$-th row from the top and the $j$-th column from the left.
Determine if it is possible to reach a state where, for all pairs of integers $(i,j)$ $(1 \leq i \leq H, 1 \leq j \leq W)$,
the cell $(i,j)$ contains the integer $((i-1) \times W + j)$ by repeating the following operation at most $20$ times (possibly zero).
If it is possible, print the minimum number of operations required.
If it is impossible in $20$ or fewer operations (including the case where it is impossible no matter how many times the operation is repeated), print $-1$.
Operation: Choose a rectangle of size $(H-1) \times (W-1)$ from the grid and rotate it $180$ degrees.
More precisely, choose integers $x$ and $y$ $(0 \leq x, y \leq 1)$,
and for all pairs of integers $(i,j)$ satisfying $1 \leq i \leq H-1$ and $1 \leq j \leq W-1$,
simultaneously replace the integer written in cell $(i+x,j+y)$ with the number written in cell $(H-i+x,W-j+y)$.
Note that it is only necessary for the integers written in the cells to satisfy the condition; the orientation in which they are written does not matter.
Specifically, for $1 \leq i \leq H$ and $1 \leq j \leq W$, the cell at the $i$-th row from the top and the $j$-th column from the left contains $S_{i,j}$.
Below, let $(i,j)$ denote the cell at the $i$-th row from the top and the $j$-th column from the left.
Determine if it is possible to reach a state where, for all pairs of integers $(i,j)$ $(1 \leq i \leq H, 1 \leq j \leq W)$,
the cell $(i,j)$ contains the integer $((i-1) \times W + j)$ by repeating the following operation at most $20$ times (possibly zero).
If it is possible, print the minimum number of operations required.
If it is impossible in $20$ or fewer operations (including the case where it is impossible no matter how many times the operation is repeated), print $-1$.
Operation: Choose a rectangle of size $(H-1) \times (W-1)$ from the grid and rotate it $180$ degrees.
More precisely, choose integers $x$ and $y$ $(0 \leq x, y \leq 1)$,
and for all pairs of integers $(i,j)$ satisfying $1 \leq i \leq H-1$ and $1 \leq j \leq W-1$,
simultaneously replace the integer written in cell $(i+x,j+y)$ with the number written in cell $(H-i+x,W-j+y)$.
Note that it is only necessary for the integers written in the cells to satisfy the condition; the orientation in which they are written does not matter.
Input
The input is given from Standard Input in the following format:
```
$H$ $W$
$S_{1,1}$ $S_{1,2}$ $\ldots$ $S_{1,W}$
$S_{2,1}$ $S_{2,2}$ $\ldots$ $S_{2,W}$
$\vdots$
$S_{H,1}$ $S_{H,2}$ $\ldots$ $S_{H,W}$
```
```
$H$ $W$
$S_{1,1}$ $S_{1,2}$ $\ldots$ $S_{1,W}$
$S_{2,1}$ $S_{2,2}$ $\ldots$ $S_{2,W}$
$\vdots$
$S_{H,1}$ $S_{H,2}$ $\ldots$ $S_{H,W}$
```
Output
Print the minimum number of operations required to meet the conditions of the problem statement.
If it is impossible to satisfy the conditions with $20$ or fewer operations, output $-1$.
If it is impossible to satisfy the conditions with $20$ or fewer operations, output $-1$.
Constraints
- $3 \leq H,W \leq 8$
- $1 \leq S_{i,j} \leq H \times W$
- If $(i,j) \neq (i',j')$, then $S_{i,j} \neq S_{i',j'}$
- All input values are integers.
- $1 \leq S_{i,j} \leq H \times W$
- If $(i,j) \neq (i',j')$, then $S_{i,j} \neq S_{i',j'}$
- All input values are integers.
Sample 1 Input
3 3
9 4 3
2 1 8
7 6 5
Sample 1 Output
2
Operating in the following order will satisfy the conditions of the problem statement in 2 operations.
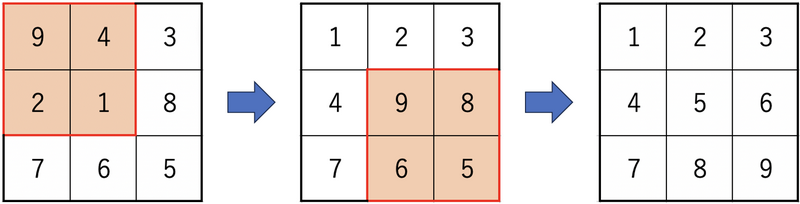
- Operate by choosing the rectangle in the top-left corner. That is, by choosing x=0 and y=0.
- Operate by choosing the rectangle in the bottom-right corner. That is, by choosing x=1 and y=1.

Sample 2 Input
4 6
15 18 1 14 3 4
23 24 19 8 9 12
13 2 17 6 5 16
21 22 7 20 11 10
Sample 2 Output
-1
It is impossible to satisfy the conditions with 20 or fewer operations, so print -1.
Sample 3 Input
4 6
1 4 13 16 15 18
21 20 9 12 23 10
17 14 5 6 3 2
11 22 7 24 19 8
Sample 3 Output
20
4 3
1 2 3
4 5 6
7 8 9
10 11 12
0
HINT
相同题目:ABC336。