9102: CCC '23 S5 - The Filter
[Creator : ]
Description
Canadian Computing Competition: 2023 Stage 1, Senior #5
Alice, the mathematician, likes to study real numbers that are between 0 and 1. Her favourite tool is the filter.
A filter covers part of the number line. When a number reaches a filter, two events can happen. If a number is not covered by the filter, the number will pass through. If a number is covered, the number will be removed.
Alice has infinitely many filters. Her first 3 filters look like this:
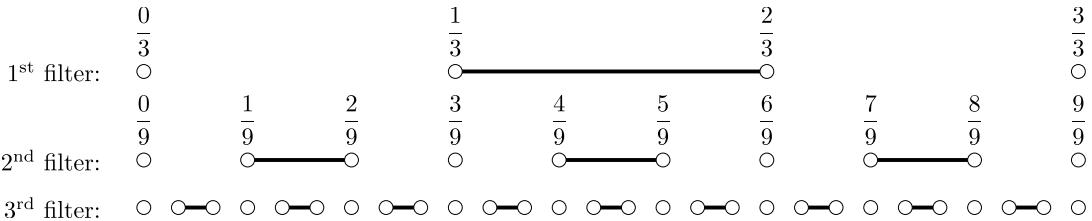
In general, the $k$-th filter can be defined as follows:
- Consider the number line from 0 to 1.
- Split this number line into $3^k$ equal-sized pieces. There are $3^k+1$ points and $3^k$ intervals.
- The $k$-th filter consists of the $2^{nd}$ interval, $5^{th}$ interval, $8^{th}$ interval, and in general, the $(3i−1)^{th}$ interval. The points are not part of the $k$-th filter.
Alice wants to research the Cantor set, and she came to you for help. Given an integer $N$, Alice would like to know which fractions $\frac{x}{N}$ are in the Cantor set.
Input
The first line contains the integer $N$.
The following table shows how the available 15 marks are distributed:
The following table shows how the available 15 marks are distributed:
| Marks Awarded | Bounds on N | Additional Constraints |
|---|---|---|
| 3 marks | $3≤N≤3^{18}$ | $N$ is a power of 3 |
| 4 marks | $2≤N≤10^5$ | None |
| 8 marks | $2≤N≤10^9$ | None |
Output
Output all integers $x$ where $0≤x≤N$ and $\frac{x}{N}$ is in the Cantor set.
Output the answers in increasing order. The number of answers will not exceed $10^6$.
Output the answers in increasing order. The number of answers will not exceed $10^6$.
Sample 1 Input
12
Sample 1 Output
0
1
3
4
8
9
11
12
Here is a diagram of the fractions and the first 4 filters. In reality, there are infinitely many filters.
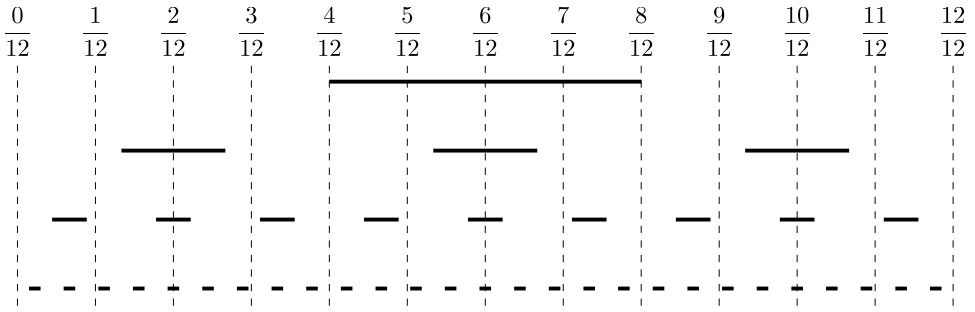
$\frac{5}{12},\frac{6}{12}$ and $\frac{7}{12}$ are not in the Cantor set because they were covered by the $1^{st}$ filter.
Furthermore, $\frac{2}{12}$ and $\frac{10}{12}$ are not in the Cantor set because they were covered by the $2^{nd}$ filter.
It can be shown that the remaining fractions will pass through all filters.

$\frac{5}{12},\frac{6}{12}$ and $\frac{7}{12}$ are not in the Cantor set because they were covered by the $1^{st}$ filter.
Furthermore, $\frac{2}{12}$ and $\frac{10}{12}$ are not in the Cantor set because they were covered by the $2^{nd}$ filter.
It can be shown that the remaining fractions will pass through all filters.