1. [J-2017-11]对于给定的序列{ak}，我们把 (i, j) 称为逆序对当且仅当 i < j 且 ai > aj。那么 序列 1, 7, 2, 3, 5, 4 的逆序对数为（ ）个。

 A. 4

 B. 5

 C. 6

 D. 7

2. [S-2014-12]同时查找 2n 个数中的最大值和最小值，最少比较次数为（ ）.

 A. 3(n−2)/2 

 B. 4n-2

 C. 3n-2

 D. 2n-2

3. [J-2018-10][J-2013-3][S-2013-3]下面的故事与（ ）算法有着异曲同工之妙。 从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事：从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事：‘从前有座山，山里有座庙，庙里有个老和尚给小和尚讲故事....’

 A. 枚举

 B. 递归

 C. 贪心

 D. 分治

4. [J-2014-18]设有100个数据元素，采用折半搜索时，最大比较次数为( )。

 A. 6

 B. 7

 C. 8

 D. 10

5. [S-2017-12]在 n(n≥3) 枚硬币中有一枚质量不合格的硬币（质量过轻或质量过重）,如果只有一架天平可以用来称重且称重的硬币数没有限制，下面是找出这枚不合格的硬币的算法。请把 a-c 三行代码补全到算法中。

a. A ← X ∪ Y

b. A ← Z

c. n ← |A|

算法 Coin(A, n)

1. k ← ⌊n/3⌋   

2. 将 A 中硬币分成 X，Y，Z 三个集合，使得 |X| = |Y| = k,|Z| = n - 2k  

3. if W(X) ≠ W(Y)  //W(X), W(Y) 分别为 X 或 Y 的重量   

4. then __________   

5. else __________   

6.   ___  

7. if n>2 then goto 1   

8. if n=2 then 任取 A 中 1 枚硬币与拿走硬币比较，若不等，则它不合格； 若相等，则 A 中剩下的硬币不合格.    

9.  if n=1 then A 中硬币不合格   

正确的填空顺序是（ ）。

 A. b, c, a

 B. c, b, a

 C. c, a, b

 D. a, b, c

6. [S-2019-15][S-2017-13]正实数构成的数字三角形排列形式如图所示。第一行的数为a[1][1]，第二行的数从左到右依次为a[2][1], a[2][2]，第 n 行的数为a[n][1], a[n][2], ..., a[n][n]。

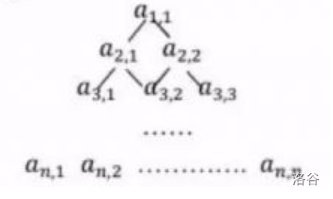
从a[1][1] 开始，每一行的数a[i][j]  只有两条边可以分别通向下一行的两个数a[i+1][j]和a[i+1][j+1]。用动态规划算法找出一条从a[1][1]向下通到a[n][1], a[n][2], ..., a[n][n]中某个数的路径，使得该路径上的数之和最大。

令 C[i][j] 是从a[1][1]到a[i][j] 的路径上的数的最大和，并且 C[i][0]=C[0][j]=0C[i][0]=C[0][j]=0，则 C[i][j]=( )。

A. max(C[i-1][j-1], C[i-1][j])+a[i][j]

B. C[i-1][j-1]+C[i-1][j]

C. max(C[i-1][j-1], C[i-1][j])+1

D. max(C[i][j-1], C[i-1][j])+a[i][j]  

7. [J-2011-17]（ ）是一种选优搜索法，按选优条件向前搜索，以达到目标。当搜索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择。

 A. 回溯法

 B. 枚举法

 C. 动态规划

 D. 贪心

8. [S-2020-6]下列哪些问题不能用贪心法精确求解？（ ）

 A. 霍夫曼编码问题

 B.  0-1 背包问题

 C. 最小生成树问题

 D. 单源最短路径问题

9. [J-2021-13]考虑如下递归算法

solve(n)  

     if n<=1 return 1  

      else if n>=5 return n*solve(n-2)  

      else return n*solve(n-1)  

则调用 solve(7) 得到的返回结果为（ ）。

 A. 105

 B. 840

 C. 210

 D. 420

10. [S-2021-3][S-2012-7]在程序运行过程中，如果递归调用的层数过多，可能会由于（ ）引发错误。

 A. 系统分配的栈空间溢出

 B. 系统分配的队列空间溢出

 C. 系统分配的链表空间溢出

 D. 系统分配的堆空间溢出