8357: 学习系列 —— 容斥原理
[Creator : ]
Description
【入门例题】
假设班里有
$10$ 个学生喜欢数学，$15$ 个学生喜欢语文，$21$ 个学生喜欢编程，班里至少喜欢一门学科的有多少个学生呢？ 【解析】
为了叙述方便，我们把喜欢语文、数学、编程的学生集合分别用$A,B,C$ 表示，则学生总数等于 $|A \cup B\cup C|$。刚才已经讲过，如果把这三个集合的元素个数 $|A|,|B|,|C|$ 直接加起来，会有一些元素重复统计了，因此需要扣掉 $|A\cap B|,|B\cap C|,|C\cap A|$，但这样一来，又有一小部分多扣了，需要加回来，即 $|A\cap B \cap C|$。即 $|A \cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|B\cap C|-|C\cap A|+|A\cap B \cap C|$
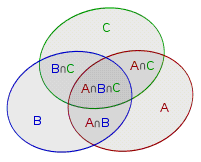
把上述问题推广到一般情况，就是我们熟知的容斥原理。
【定义】
设 U 中元素有 n 种不同的属性，而第 i 种属性称为$P_i$，拥有属性 $P_i$ 的元素构成集合 $S_i$，那么 $|\cup_{i=1}^{n} S_i|=\sum_{i} |S_i|-\sum_{i<j} |S_i \cap S_j|+\sum_{i<j<k} |S_i \cap S_j \cap S_k|- \cdots+(-1)^{m-1}\sum_{a_i<a_{i+1}}|\cap_{i=1}^{m}S_{a_i}+\cdots+(-1)^{n-1}|S_1\cap \cdots \cap S_n||$
即
$|\cup_{i=1}^{n} S_i|=\sum_{m=1}^{n} (-1)^{m-1} \sum_{a_i<a_{i+1}}|\cap_{i=1}^m S_{a_{i}}|$