8298: 学习系列 —— OI内的排列与组合
[Creator : ]
Description
【加法原理】
做一件事,完成它可以有 $n$ 类方法,在第一类办法中有 $m_1$ 种不同的方法,在第二类办法中有 $m_2$ 种不同的方法,……。在第 $n$ 类办法中有 $m_n$ 种不同的方法,那么完成这件事共有:$N = m_1+m_2+…+m_n$ 种不同的方法。
【例题】
问:从甲地到乙地,可以乘火车,也可以乘汽车,还可以乘轮船。一天中,火车有 4 班,汽车有 2 班,轮船有 3 班。那么,一天中乘坐这些交通工具从甲地到乙地共有多少种不同走法?分析:因为从甲地到乙地,乘火车有 4 种选择(方法),乘汽车有 2 种选择(方法),乘轮船有 3 种选择(方法)。因此,一天中乘坐这些交通工具从甲地到乙地共有:4+2+3 = 9 种不同的方法。
【乘法原理】
做一件事,完成它需要分成 $n$ 个步骤,做第一步有 $m_1$ 种不同方法,做第二步有 $m_2$ 种不同方法,……,做第 $n$ 步有 $m_n$ 种不同方法。那么完成这件事共有 $m_1\times m_2\times \cdots \times m_n$ 种不同的方法。
【例题】
问:由A村去B村的道路有3条,由B村去C村的道路有2条(如下图所示)。从A村经B村去C村,共有多少种不同的走法?如下图所示。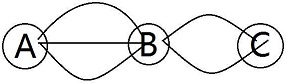
分析:从 A 村到 B 村有 3 种不同的走法,按这 3 种走法中的每一种走法到达 B 村后,再从 B 村到 C 村又有 2 种不同的走法。因此,从 A 村经 B 村去 C 村共有:3×2 = 6种不同的走法。