Description

【定义】

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小。

【性质】

以树的重心为根时，所有子树的大小都不超过整棵树大小的一半。
树中所有点到某个点的距离和中，到重心的距离和是最小的；如果有两个重心，那么到它们的距离和一样。
把两棵树通过一条边相连得到一棵新的树，那么新的树的重心在连接原来两棵树的重心的路径上。
在一棵树上添加或删除一个叶子，那么它的重心最多只移动一条边的距离。

【样例】

如下图所示，以 $1$ 为根节点的树。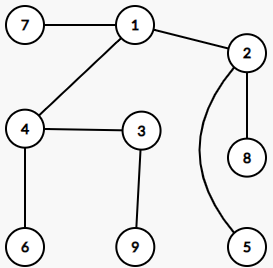

删除节点 1，有 3 个联通块，最大的联通块数量为 4。
删除节点 2，有 2 个联通块，最大的联通块数量为 6。
删除节点 3，有 2 个联通块，最大的联通块数量为 6。
删除节点 4，有 3 个联通块，最大的联通块数量为 5。
删除节点 5，有 1 个联通块，最大的联通块数量为 8。
删除节点 6，有 1 个联通块，最大的联通块数量为 8。
删除节点 7，有 1 个联通块，最大的联通块数量为 8。
删除节点 8，有 1 个联通块，最大的联通块数量为 8。
删除节点 9，有 1 个联通块，最大的联通块数量为 8。
因此，这颗树的重心是 4。

【时间复杂度】

$O(n+m)$。

Input

【过程】

给定一颗树，树中包含 n 个结点（编号 1～n）和 n-1 条无向边。

【初始状态】

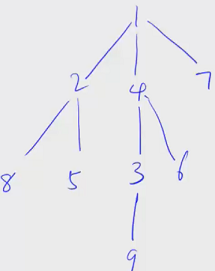
我们依次枚举将各点删除后，剩余每个连通块中节点数的最大值。

【删除节点 1】

比如我们将 1 号根节点删掉，剩下了 3 个连通块，其中连通块中节点数最大值为 4（包含4、3、6、9六个节点）。如下图所示。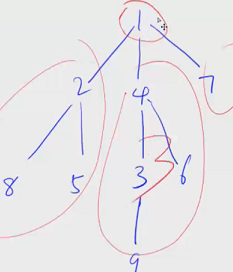

【删除节点 2】

如果我们将 2 号节点删去，同样剩余 3 个连通块，其中连通块中节点数最大值为 6（包含1、4、7、3、6、9六个节点）。如下图所示。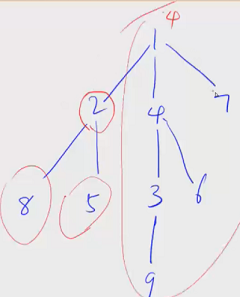

【删除节点 4】

同样的道理，我们将 4 号节点删去，也剩余 3 个连通块，其中连通块中节点数最大值为 5（包含1、2、7、8、5五个节点）。如下图所示。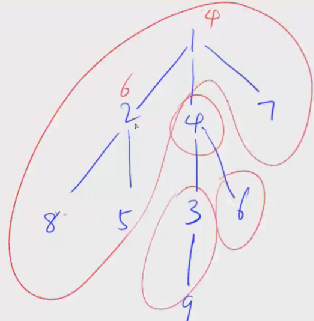

【答案】

其他的节点这里就不作分析了，
我们的目标是求出并输出“最小的最大值”，经过树中所有点的枚举，我们可以得出最优解就是 4，即将树中的重心删除后，剩余各连通块中点数最大值为 4。

Output

【代码实现】

【C++】

const int N = 1e5+10;
int n;
bool st[N];
int h[N], e[N<<1], ne[N<<1], idx, sz[N];
int ans; //设置一个全局的答案，存储“最小的最大值”

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

int dfs(int u) //返回以 u 为子树的大小
{
    int res = 0; //存储将该点删去之后，剩余各连通块大小的最大值
    sz = 1; //当前点算 1 个点，所以从 1 开始
    st = true;
    for(int i=h; ~i; i=ne[i]) {
        int j = e[i];
        if(!st[j]) {
            int s = dfs(j); //子树 j 大小
            res = max(res, s); //子树 j 是个连通块，将它的大小与 res 取 max
            sz += s; //子树 j 是子树 u 的一部分，因此 sz 要加上子树 j 大小
        }
    }
    res = max(res, n-sz); //n-sz 即上文提到的节点 u “父节点及以上部分” 的大小，也是个连通块，用其大小更新 res
    ans = min(ans, res); //更新全局答案
    return sz; 
}

void solve() {
    cin>>n;
    ans = n;
    memset(h, -1, sizeof h);
    for(int i=0; i<n-1; ++i) {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a); //无向边
    }
    dfs(1);
    cout<<ans<<"\n";
}

8286: 学习系列 —— 树上问题 —— 树的重心