8285: 学习系列 —— 树上问题 —— 树的直径，树的中心
[Creator : ]
Description
【定义】
树的直径，又称树的最长链，定义为一棵树上最远的两个节点的路径，即树上一条不重复经过某一条边的最长的路径。树的直径也可以代指这条路径的长度。显然，一棵树可以有多条直径，他们的长度相等。
可以用两次 DFS 或者树形 DP 的方法在 $O(n)$
时间求出树的直径。 Input
【两次 DFS】
首先从任意节点 $y$ 开始进行第一次 DFS，到达距离其最远的节点，记为 $x$。然后再从 $x$
开始做第二次 DFS，到达距离 $z$ 最远的节点，记为 $z^\prime$，则 $\delta(z,z^\prime)$ 即为树的直径。显然，如果第一次 DFS 到达的节点 $z$
是直径的一端，那么第二次 DFS 到达的节点 $z^\prime$ 一定是直径的一端。我们只需证明在任意情况下，$z$ 必为直径的一端。定理：在一棵树上，从任意节点
$y$ 开始进行一次 DFS，到达的距离其最远的节点 $z$ 必为直径的一端。【证明】
使用反证法。记出发节点为 $y$。设真实的直径是 $\delta(s,t)$，而从 $y$ 进行的第一次 DFS 到达的距离其最远的节点 $z$ 不为 $t$ 或 $s$。共分三种情况：-
若 $y$ 在 $\delta(s,t)$ 上：
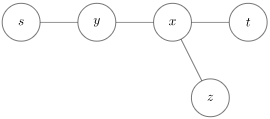
有 $\delta(y,z)>\delta(y,t)\rightarrow \delta(x,z)>\delta(x,t) \rightarrow \delta(s,z)>\delta(s,t)$
，与 $\delta(s,t)$ 为树上任意两节点之间最长的简单路径矛盾。-
若 $y$ 不在 $\delta(s,t)$ 上，且 $\delta(y,z)$ 与 $\delta(s,t)$ 存在重合路径：
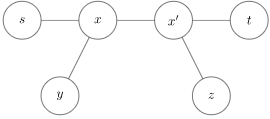
有
$\delta(y,z)>\delta(y,t)\rightarrow \delta(x,z)>\delta(x,t) \rightarrow \delta(s,z)>\delta(s,t)$，与 $\delta(s,t)$ 为树上任意两节点之间最长的简单路径矛盾。-
若 $y$ 不在 $\delta(s,t)$ 上，且 $\delta(y,t)$ 与 $\delta(s,t)$ 不存在重合路径：
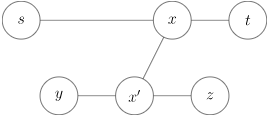
有 $\delta(y,z)>\delta(y,t)\rightarrow \delta(x^\prime,z)>\delta(x^\prime,t) \rightarrow \delta(x,z)>\delta(x,t) \rightarrow \delta(s,z)>\delta(s,t)$
，与 $\delta(s,t)$ 为树上任意两节点之间最长的简单路径矛盾。综上，三种情况下假设均会产生矛盾，故原定理得证。
特别注意：上述证明过程建立在所有路径均不为负的前提下。如果树上存在负权边，则上述证明不成立。故若存在负权边，则无法使用两次 DFS 的方式求解直径。
【代码实现】
【C++】
const int N=5e5+10;
LL h[N];
const int M=2*N;
LL e[M], w[M], ne[M], idx;
LL dis[N];//dis[i]表示到跟节点距离
LL nc;//最远的节点
void init(LL n) {
idx=0;
nc=0;
for (LL i=0;i<=n;i++) {
h[i]=-1;
dis[i]=0;
}
}
void add(LL a,LL b,LL c=1) {
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
}
//u :当前节点
//fa:父亲节点
void dfs(LL u,LL fa) {
//cout<<"u="<<u<<",fa="<<fa<<"\n";
for (LL i=h[u\];i!=-1;i=ne[i]) {
LL v=e[i];
if (v==fa) {
continue;
}
dis[v]=dis[u\]+w[i];
//记录最远的节点
if (dis[v]>dis[nc]) {
nc=v;
}
dfs(v,u);
}
}
void solve() {
LL n;
cin>>n;
init(n);
for (LL i=1;i<n;i++) {
LL a,b,c=1;
cin>>a>>b;
add(a,b,c);
add(b,a,c);
}
//找 1 最远节点 c
dfs(1,0);
//找 c 最远的节点
dis[nc]=0;
dfs(nc,0);
cout<<dis[nc]<<"\n";
}
如果需要求出一条直径上所有的节点，则可以在第二次 DFS 的过程中，记录每个点的前序节点，即可从直径的一端一路向前，遍历直径上所有的节点。
Output
【树形 DP】
【C++】
【方法 1】
我们记录当 $1$
为树的根时，每个节点作为子树的根向下，所能延伸的最长路径长度 $d_1$ 与次长路径（与最长路径无公共边）长度 $d_2$，那么直径就是对于每一个点，该点 $d_1+d_2$ 能取到的值中的最大值。 树形 DP 可以在存在负权边的情况下求解出树的直径。
const int N = 10000 + 10;
int n, c, d1[N],d2[N];
int h[N],w[N*2],e[N*2],ne[N*2],idx;
int d;
void add(int a,int b,int c) {
e[idx] = b,ne[idx] = h[a],w[idx] =c,h[a]=idx++;
}
void dfs(int u, int fa) {
d1[u\] = d2[u\] = 0;
for(int i=h[u\];~i;i=ne[i]) {
int v = e[i];
if (v == fa) continue;
dfs(v, u);
int t = d1[v] + w[i];
if(t>d1[u\])
d2[u\]=d1[u\],d1[u\] = t;
else if(t>d2[u\])
d2[u\] = t;
}
d=max(d,d1[u\]+d2[u\]);
}
void solve() {
cin>>n;
memset(h,-1,sizeof h);
for(int i=1; i<n; i++) {
int u,v,c;
cin>>u>>v>>c;
add(u,v,c);
add(v,u,c);
}
dfs(1,0);
cout<<d<<endl;
return;
}
如果需要求出一条直径上所有的节点，则可以在 DP 的过程中，记录下每个节点能向下延伸的最长路径与次长路径（定义同上）所对应的子节点，在求 $d$ 的同时记下对应的节点 ，使得 $d=d_1[u\]+d_2[u\]$，即可分别沿着从 $u$ 开始的最长路径的次长路径对应的子节点一路向某个方向（对于无根树，虽然这里指定了 $1$ 为树的根，但仍需记录每点跳转的方向；对于有根树，一路向上跳即可），遍历直径上所有的节点。 【方法 2】
我们可以直接使用一个 f[N] 来求解。LL ans;//答案
LL f[N];//f[i]表示以i为根，到其子树的叶节点最大距离
//u :当前节点
//fa:父亲节点
void dfs(LL u,LL fa) {
//cout<<"u="<<u<<",fa="<<fa<<"\n";
for (LL i=h[u\];i!=-1;i=ne[i]) {
LL v=e[i\];
if (v==fa) {
continue;
}
dfs(v,u);
LL t=f[v\]+w[i\];
//更新答案
ans=max(ans,f[u\]+t);
//更新f[u\]
if (f[u\]<t) {
f[u\]=t;
}
}
}
Constraints
【性质】
若树上所有边边权均为正，则树的所有直径中点重合证明：使用反证法。设两条中点不重合的直径分别为 $\delta(s,t)$
与 $\delta(s^\prime,t^\prime)$，中点分别为 $x$ 与 $x^\prime$。显然，$\delta(s,x)=\delta(x,t)=\delta(s^\prime,x^\prime)=\delta(x^\prime,t^\prime)$。 
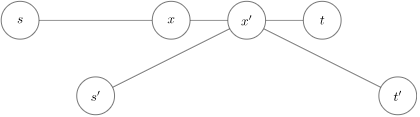
有 $\delta(s,t^\prime)=\delta(s,x)+\delta(x,x^\prime)+\delta(x^\prime,t^\prime)>\delta(s,x)+\delta(x,t)=\delta(s,t)$
，与 $\delta(s,t)$ 为树上任意两节点之间最长的简单路径矛盾，故性质得证。 【树的中心】
概念：树的直径的中点。
求法：有多种，如DP，广搜，深搜等。
简单的方法是，先求树的直径，再找到直径中点即可。
模板题：POJ3099.