Problem8284--学习系列 —— 树上问题 —— 树的基础

8284: 学习系列 —— 树上问题 —— 树的基础

[Creator : ]
Time Limit : 1.000 sec  Memory Limit : 256 MiB

SubmitSolved: 0Submit Num: 0StatisticsShowOff!

Description

【定义】

它是由 $n\ (n\ge 1)$ 个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。
它具有以下的特点：每个结点有零个或多个子结点；没有父结点的结点称为根结点；每一个非根结点有且只有一个父结点；除了根结点外，每个子结点可以分为多个不相交的子树；
树结构是一种非线性存储结构，存储的是具有“一对多”关系的数据元素的集合。

【常见概念】

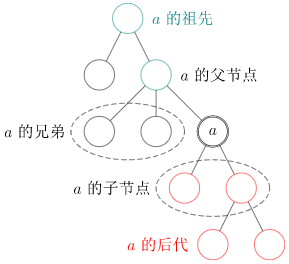
  • 父亲（parent node）：对于除根以外的每个结点，定义为从该结点到根路径上的第二个结点。 根结点没有父结点。
  • 祖先（ancestor）：一个结点到根结点的路径上，除了它本身外的结点。 根结点的祖先集合为空。
  • 子结点（child node）：如果 $u$ 是 $v$ 的父亲，那么 $v$ 是 $u$ 的子结点。子结点的顺序一般不加以区分，二叉树是一个例外。
  • 结点的深度（depth）：到根结点的路径上的边数。
  • 树的高度（height）：所有结点的深度的最大值。
  • 兄弟（sibling）：同一个父亲的多个子结点互为兄弟。
  • 后代（descendant）：子结点和子结点的后代。或者理解成：如果 $u$ 是 $v$ 的祖先，那么 $v$ 是 $u$ 的后代。

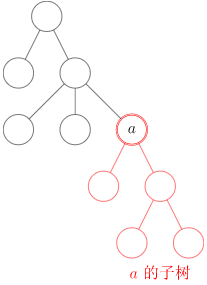
  • 子树（subtree）：删掉与父亲相连的边后，该结点所在的子图。

【特殊的树】

  • 有根二叉树（rooted binary tree）：每个结点最多只有两个儿子（子结点）的有根树称为二叉树。常常对两个子结点的顺序加以区分，分别称之为左子结点和右子结点。
    大多数情况下，二叉树 一词均指有根二叉树。
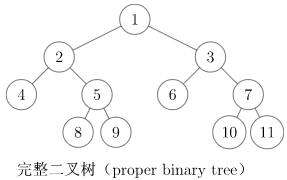
  • 完整二叉树（full/proper binary tree）：每个结点的子结点数量均为 0 或者 2 的二叉树。换言之，每个结点或者是树叶，或者左右子树均非空。

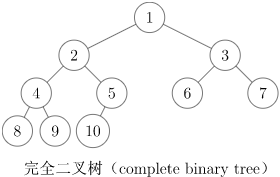
  • 完全二叉树（complete binary tree）：只有最下面两层结点的度数可以小于 2，且最下面一层的结点都集中在该层最左边的连续位置上。

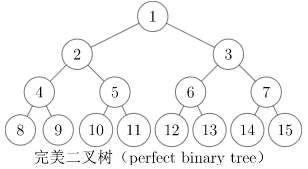
  • 完美二叉树（perfect binary tree）：所有叶结点的深度均相同的二叉树称为完美二叉树。

Input

【树的存储】

【只存储父节点】

用一个数组 parent[N] 记录每个结点的父亲结点。 
LL parent[N];
 这种方式可以获得的信息较少，不便于进行自顶向下的遍历。常用于自底向上的递推问题中。

【邻接表】

【无根树】

为每个结点开辟一个线性列表，记录所有与之相连的结点。 
std::vector<LL> adj[N];

【有根树】

方法一：若给定的是无向图，则仍可以上述形式存储。下文将介绍如何区分结点的上下关系。
方法二：若输入数据能够确保结点的上下关系，则可以利用这个信息。为每个结点开辟一个线性列表，记录其所有子结点；若有需要，还可在另一个数组中记录其父结点。 
std::vector<LL> children[N];//保存儿子节点
LL parent[N];//保存父节点

【左右孩子表示法】

【普通树】

每个结点记录两个值：其 第一个子结点 child 和其 下一个兄弟结点 sib。若没有子结点，则 child 为空；若该结点是其父结点的最后一个子结点，则 sib 为空。
遍历一个结点的所有子结点可由如下方式实现。 
int v = child;  // 从第一个子结点开始
while (v != EMPTY_NODE) {
  // ...
  // 处理子结点 v
  // ...
  v = sib[v];  // 转至下一个子结点，即 v 的一个兄弟
}

【二叉树】

需要记录每个结点的左右子结点。 
LL parent[N];
LL lch[N], rch[N];
// -- or --
LL child[N][2];

Output

【树上 DFS】

在树上 DFS 是这样的一个过程：先访问根节点，然后分别访问根节点每个儿子的子树。
可以用来求出每个节点的深度、父亲等信息。

【先序遍历 Preorder】

按照 根，左，右 的顺序遍历二叉树。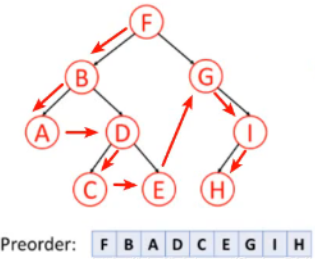

【中序遍历 Inorder】

按照 左，根，右 的顺序遍历二叉树。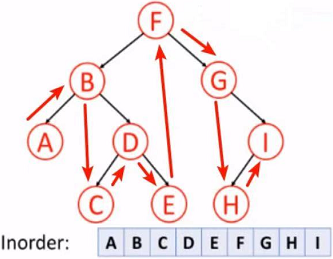

【后序遍历 Postorder】

按照 左，右，根 的顺序遍历二叉树。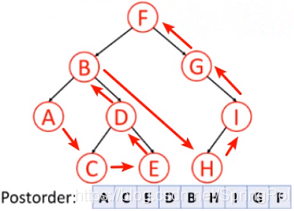

【反推】

已知中序遍历序列和另外一个序列可以求第三个序列。
前序的第一个是 root，后序的最后一个是 root。
先确定根节点，然后根据中序遍历，在根左边的为左子树，根右边的为右子树。
对于每一个子树可以看成一个全新的树，仍然遵循上面的规律。



Constraints

【树上 BFS】

从树根开始，严格按照层次来访问节点。
BFS 过程中也可以顺便求出各个节点的深度和父亲节点。

Source/Category

 
Submit