8251: 学习系列 —— 网络流 1 —— 最大流问题
[Creator : ]
Description
【概念】
一个网络 $G=(V,E)$ 是一张有向图,图中每条有向边 $(x,y)∈E$ 都有一个给定的权值 c(x,y),称为边的容量。特别地,若 $(x,y)∉E$,则 c(x,y)=0。图中还有两个指定的特殊节点 $S,T∈V(S≠T)$,分别被称为源点(S)和汇点(T)。设 f(x,y) 是定义在节点二元组 $(x,y∈V)$ 上的实数函数,且满足:
- 容量限制:f(x,y)≤c(x,y)。
- 斜对称:f(x,y)=−f(y,x)。
- 流量守恒:任意 $x≠S,x≠T,\ \sum_{(u,x)\in E}f(u,x)=\sum_{(x,v)\in E}f(x,v)$。
对于 (x,y)∈E,f(x,y) 称为边的流量,c(x,y)–f(x,y) 称为边的剩余流量。
$\sum_{(S,v)\in E}f(S,v)$ 称为整个网络的流量。
通俗地讲,我们想象一下自来水厂到你家的水管网是一个复杂的有向图,每一节水管都有一个最大承载流量。
自来水厂不放水,你家就断水了。但是就算自来水厂拼命地往管网里面注水,你家收到的水流量也是上限,毕竟每根水管承载量有限。
你想知道你能够拿到多少水,这就是一种网络流问题。
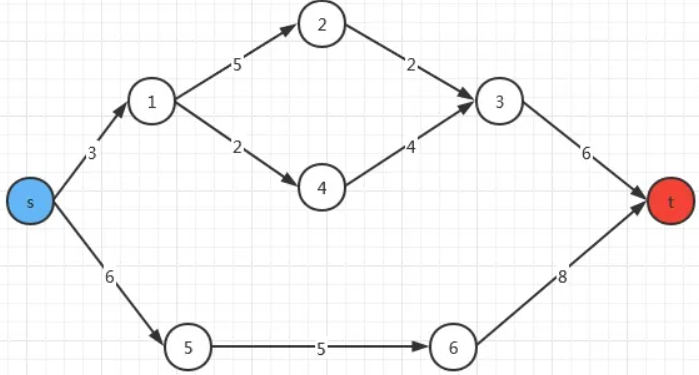
如上图中,有一个源点 S,还有一个汇点 T,边的权值称为流量。
【最大流】
对于一个给定的网络,使整个网络的流量最大的合法的流函数被称为网络的最大流,此时的流量被称为网络的最大流量。一种通俗的理解就是:把源点看成是自来水场,汇点看成你家,边就是水管,流量就是水管最多能流多少单位的水。自来水厂源源不断的放水,问你家最多能收到几个单位的水。
首先,我们从一条路径来考虑(如下图):
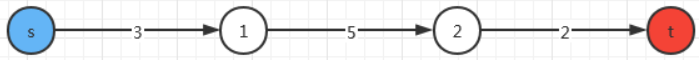
显然,最大流为2。我们发现,一条路径的流量是由这条路径的最小值决定的。
【Dinic 算法】
【时间复杂度】
$O(m\cdot n^2)$,其中 $m$ 表示图中的边数,$n$ 表示图中的顶点数量,$m\gg n$。【残量网络】
在任意时刻,网络中所有节点以及剩余容量大于 0 的边构成的子图被称为残量网络。最大流一定是阻塞流。
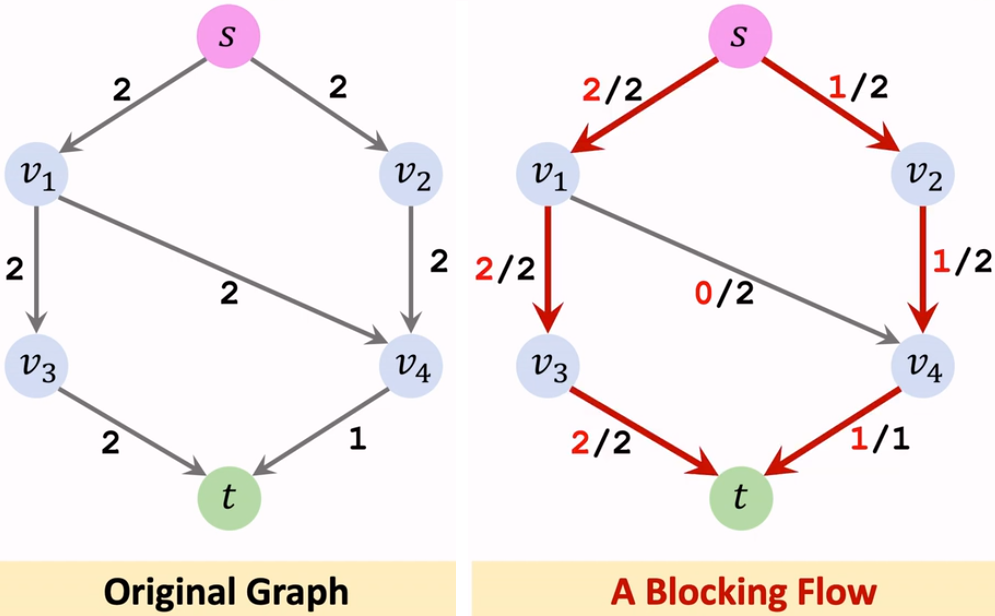
阻塞流不一定是最大流。
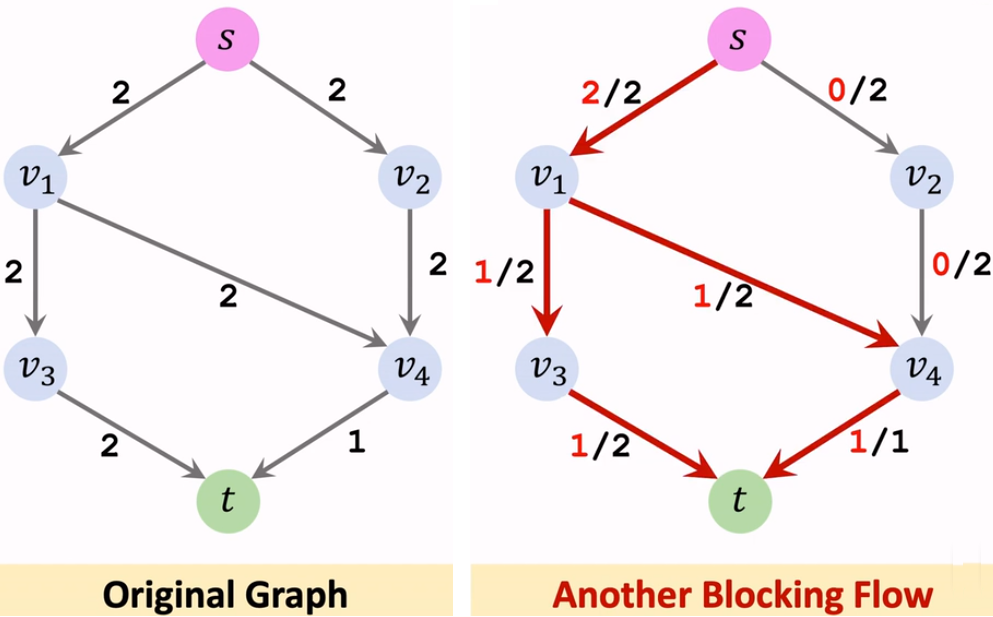
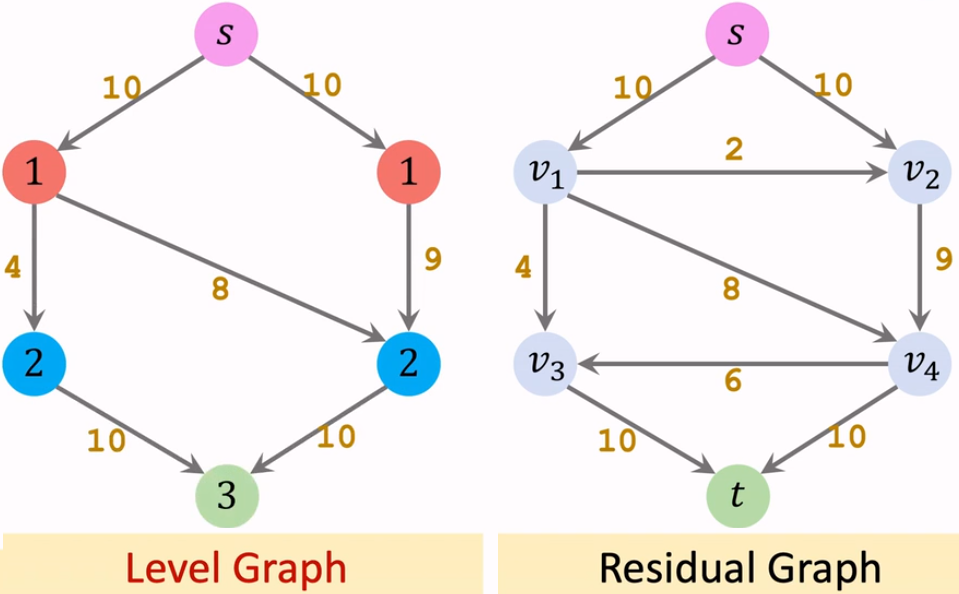
【分层图】
将图分层,节点深度 $d_x$ 表示 $S$ 到 $x$ 最少需要经过的边数。在残量网络中,满足 $d_y=d_x+1$ 的边 $(x,y)$ 构成的子图被称为分层图。
显然,分层图是一张有向无环图。
Input
【Dinic 算法】
【初始状态】
Residual Graph 就是 Original Graph 的拷贝。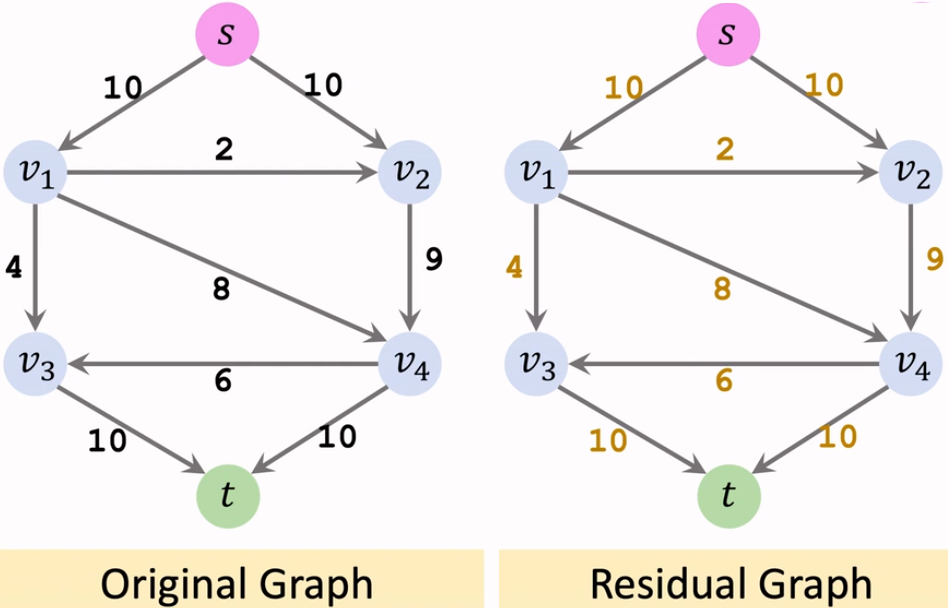
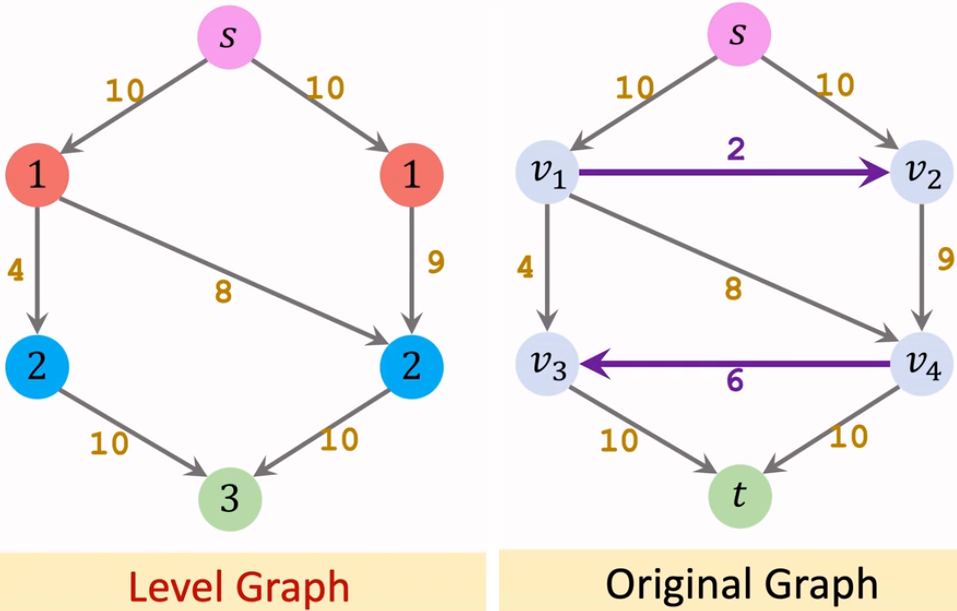
【Iteration 1: 构造分层图】
【Iteration 1: 在分层图中找阻塞流】
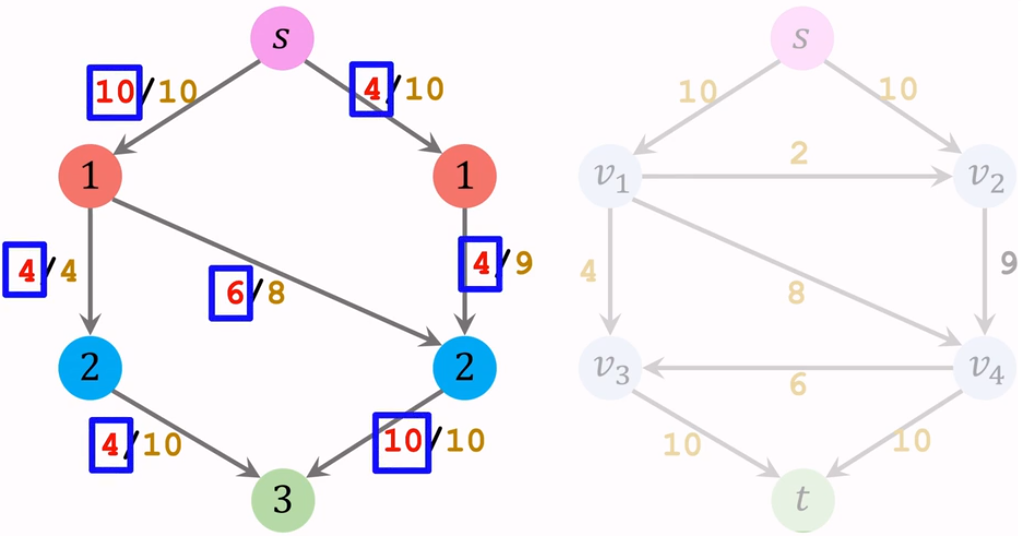
【Iteration 1: 更新残量网络】
阻塞流通过了这些管道,剩余流量就会减少。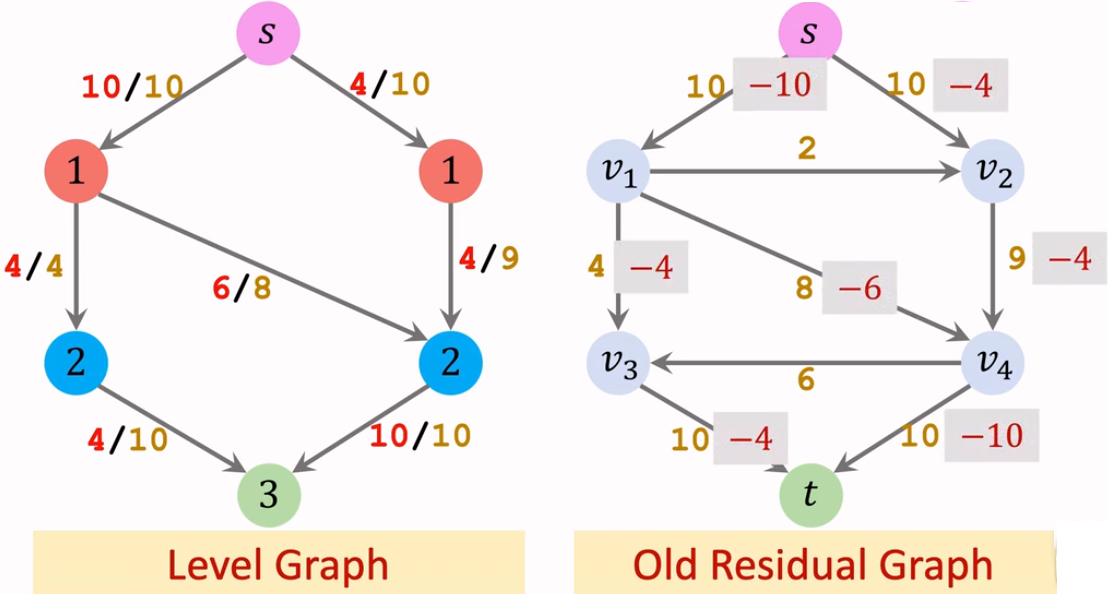
将上图残量网络中容量为 0 的路径删除,增加对应的反向流量。
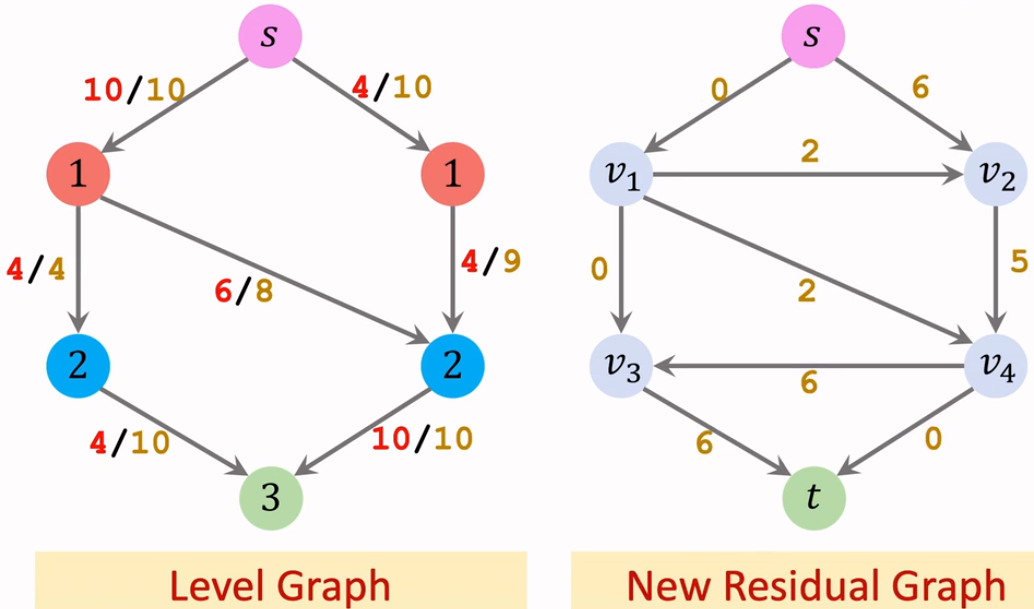
这样,我们就完成了第一次迭代。
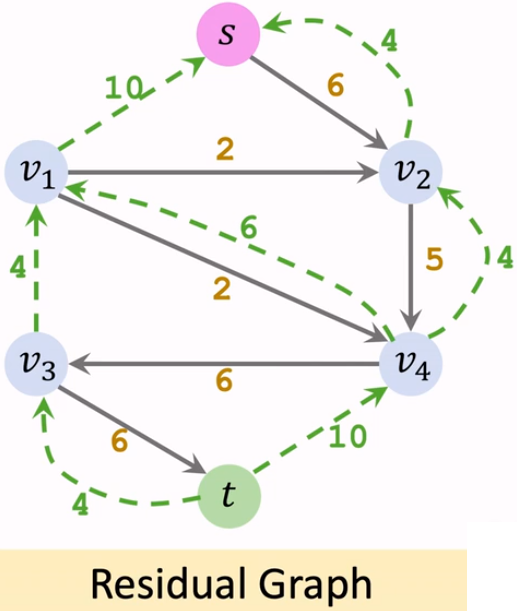
【Iteration 2: 构造分层图】
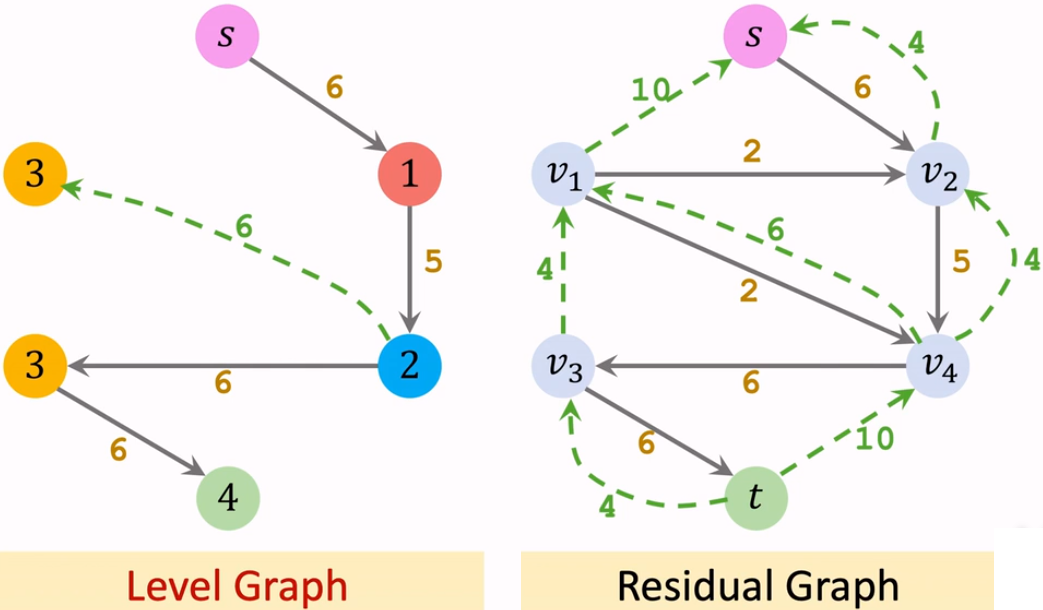
【Iteration 2: 在分层流中找阻塞流】
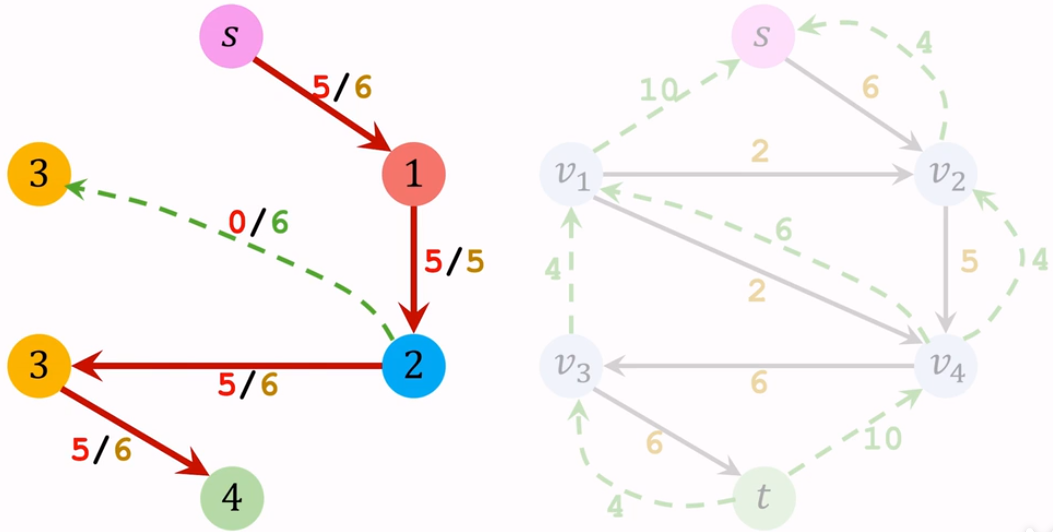
【Iteration 2: 更新残量网络】
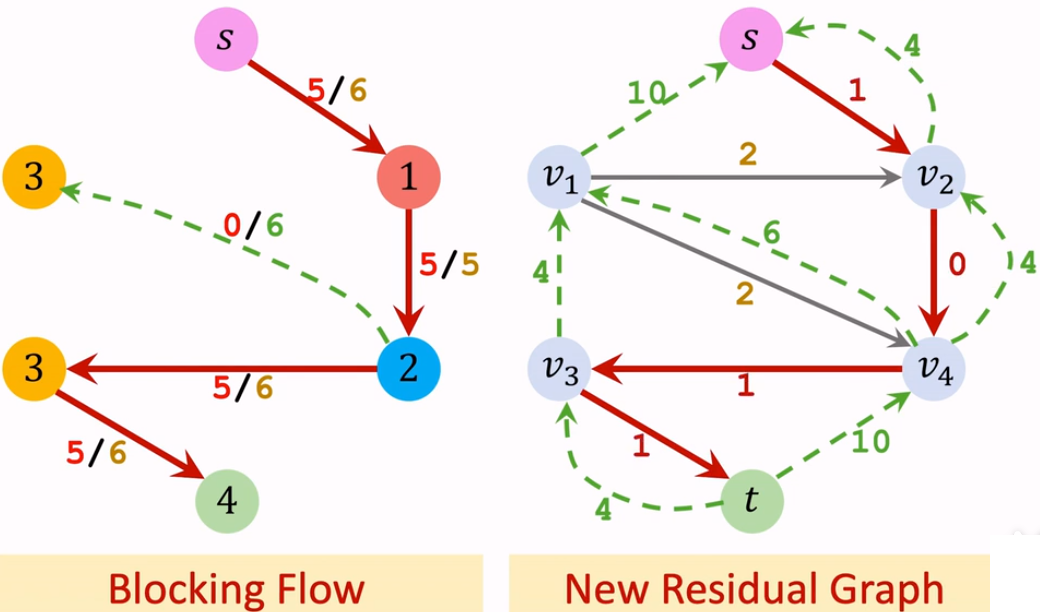
将上图残量网络中容量为 0 的路径删除,增加对应的反向流量。
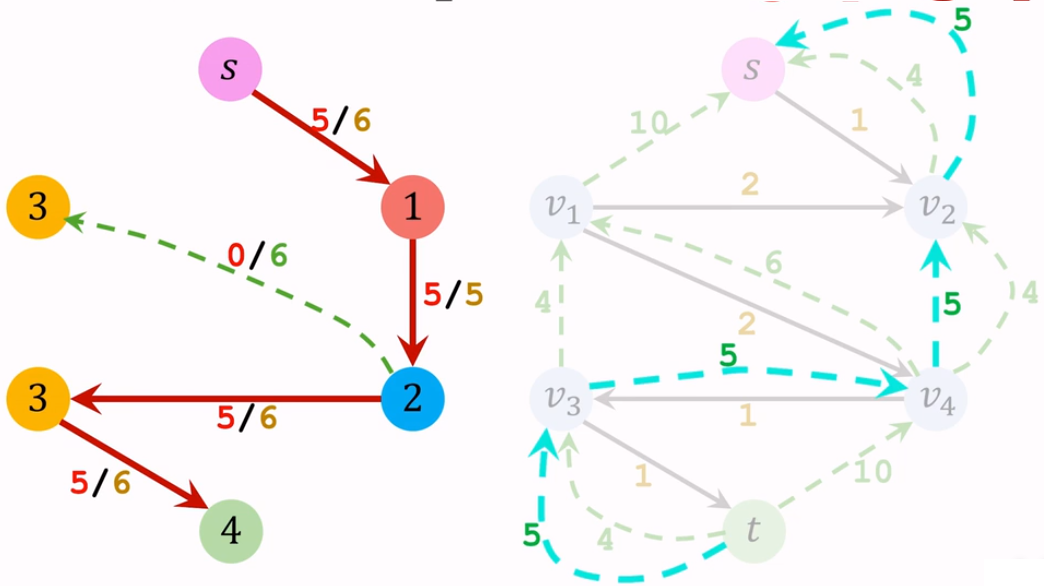
合并残量网络中的边。
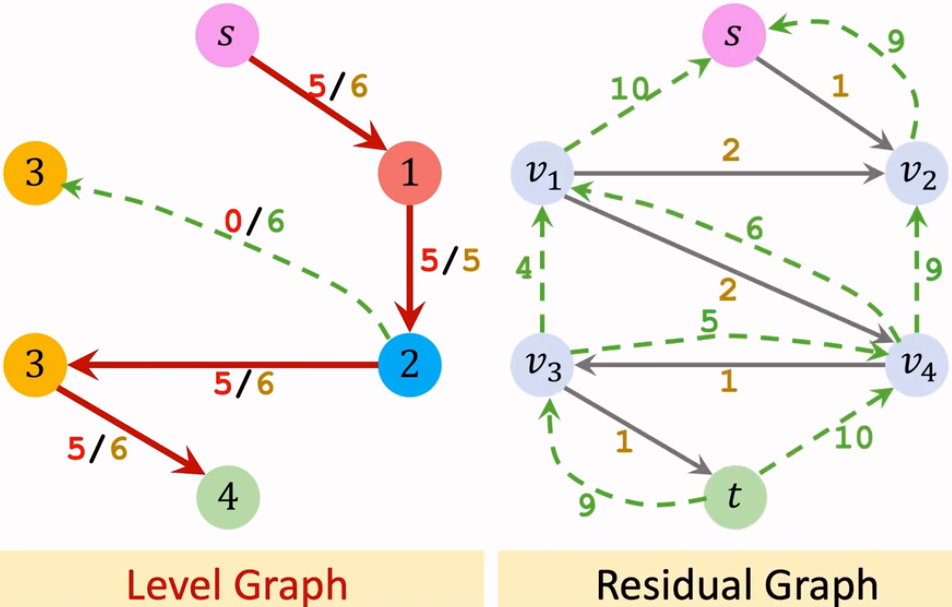
这样第二轮迭代结束。
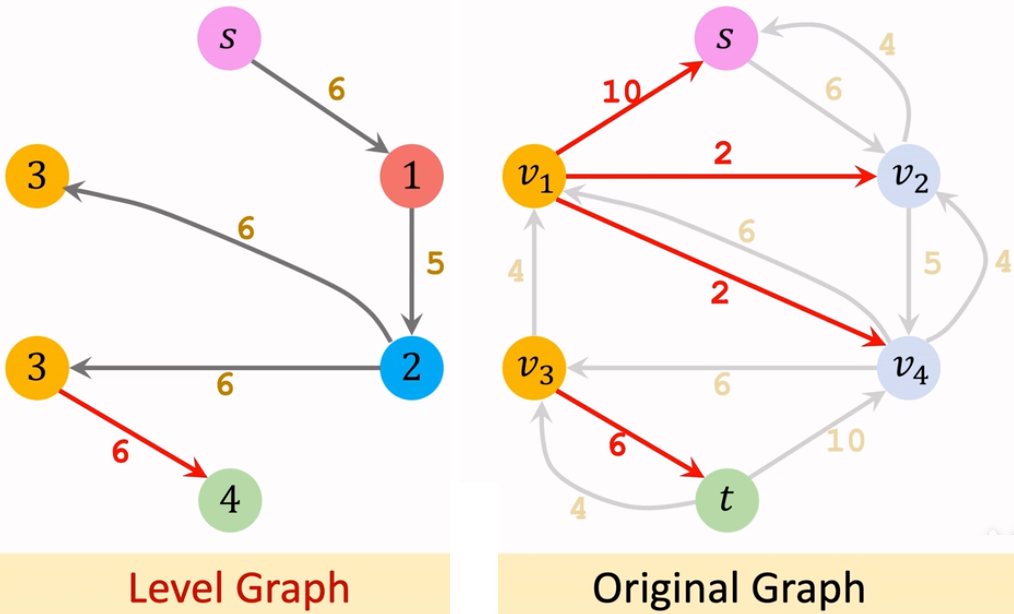
【Iteration 3: 创建分成图】
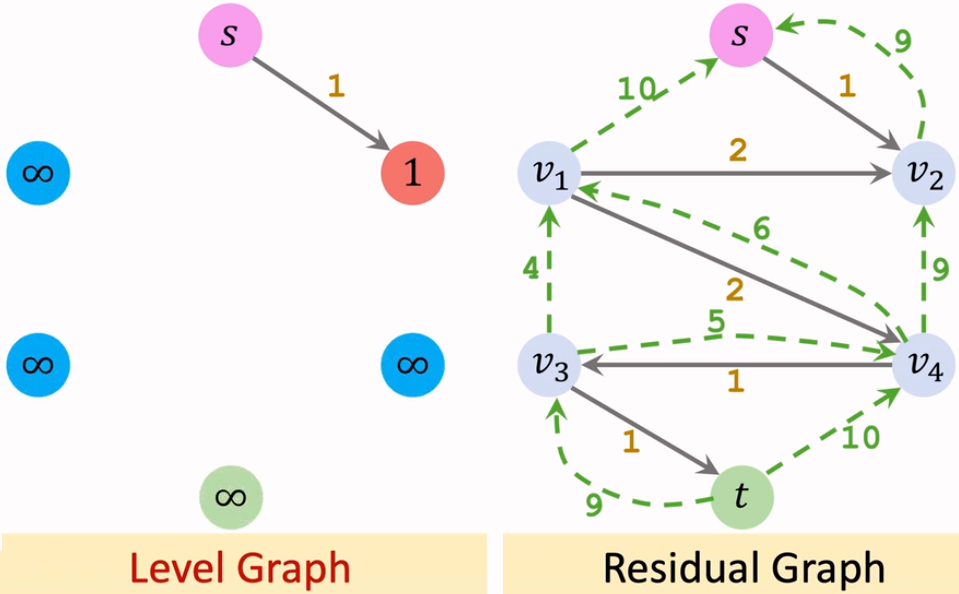
【Iteration 3: 在分层图中找阻塞流】
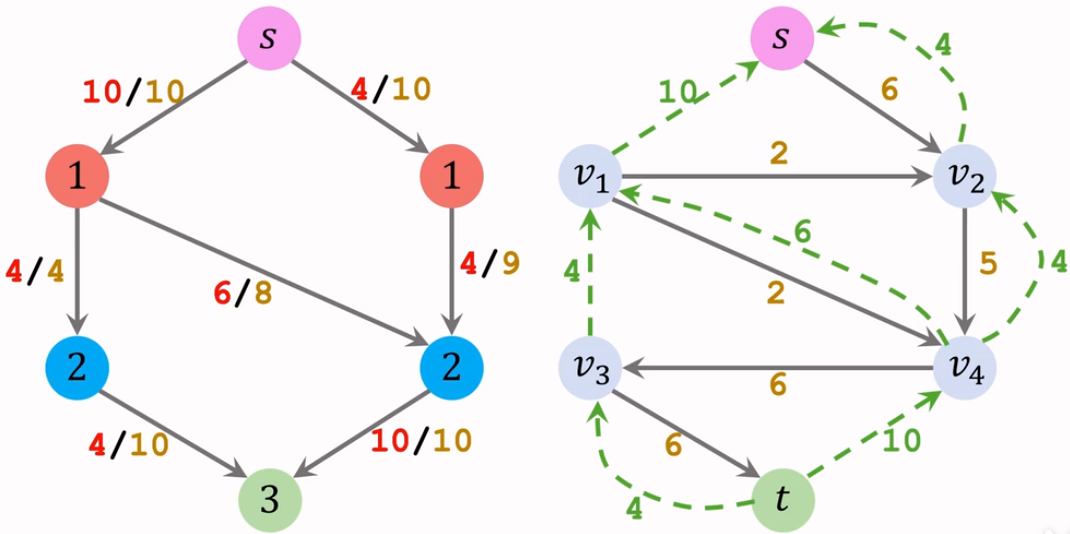
我们找不到从源点到汇点阻塞流。这样程序终止。对应的结果,就在残量网络中。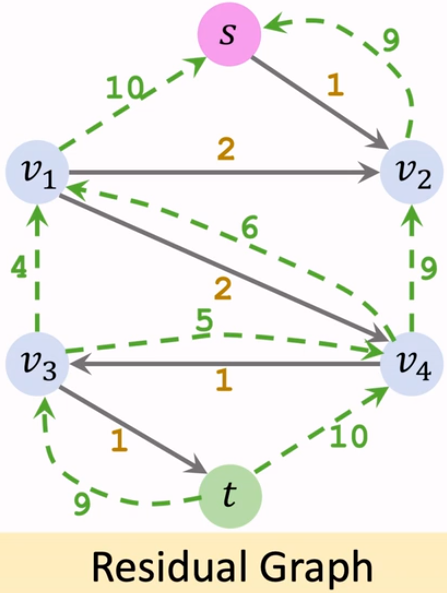
删除图中的反向路径。
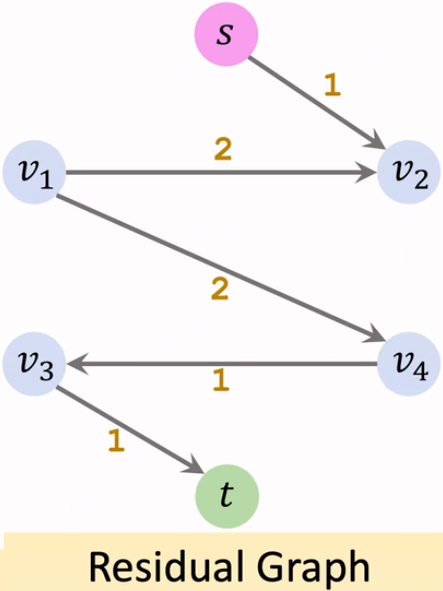
流量 = 容量 - 残量
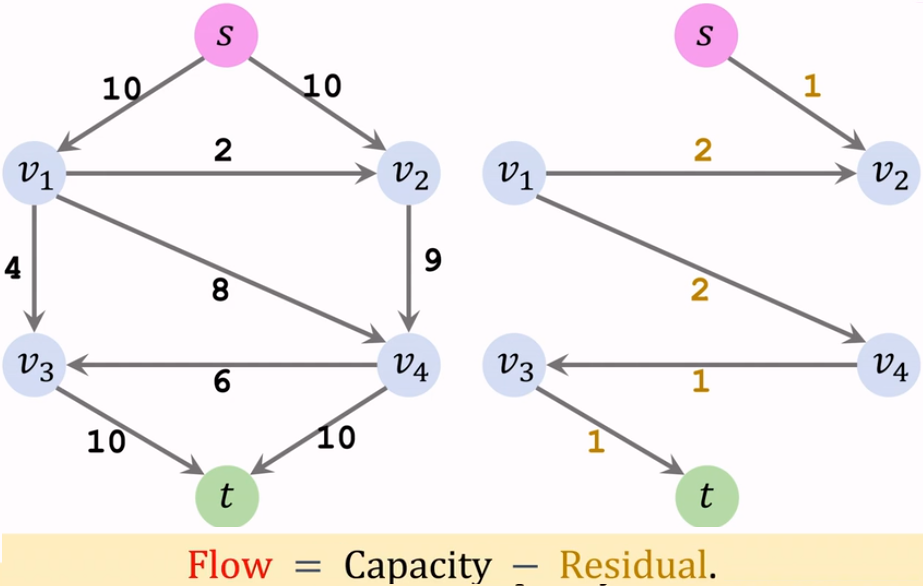
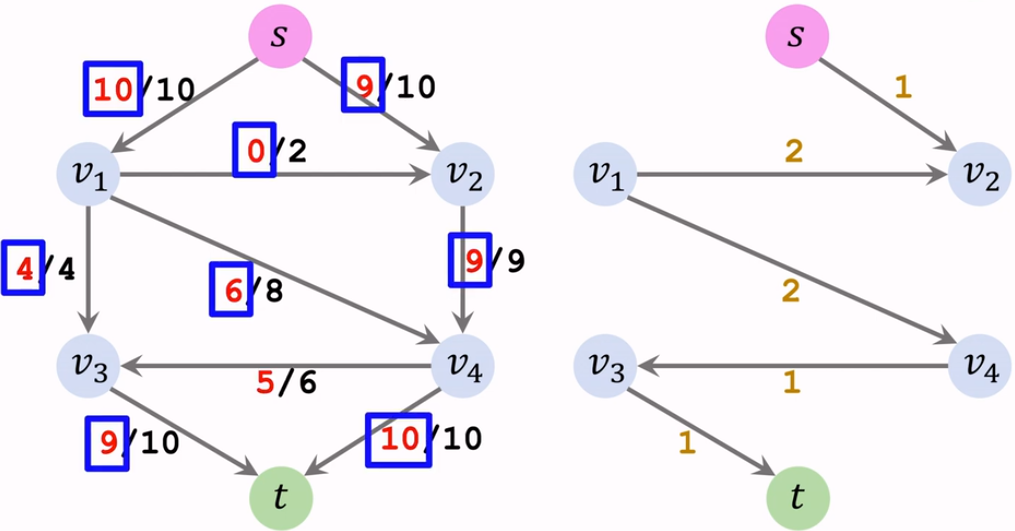
这样,上图的最大流为 $10+9=19$。
Output
【Dinic算法】
不断重复以下步骤,直到残量网络中 S 不能到达 T:
- 在残量网络上 BFS 求出节点层次,构造分层图。
- 在分层图上 DFS 寻找增广路,在回溯时实时更新剩余容量。另外,每个点可以流向多条出边,同时还加入若干剪枝及优化。
Constraints
【Dinic算法模板】
【C++】
namespace Dinic {
const LL N = 1e5 + 7, M = 2e6 + 7;
const LL INF = 9e18;
LL n, S, T, d[N];
LL h[N], hi[N];
LL e[M], ne[M], idx;
LL f[M], mxf;
inline void add(LL x, LL y, LL z, bool o = 1) {
e[idx] = y; f[idx] = z; ne[idx] = h[x]; h[x] = idx++;
if (o) {
add(y, x, 0, 0);
}
}
inline bool bfs() {
for (LL i = 1; i <= n; i++) {
d[i] = 0;
}
queue<LL> q;
q.push(S), d[S] = 1;
while (q.size()) {
LL x = q.front();
q.pop();
for (LL i = h[x]; i!=-1; i = ne[i]) {
LL y = e[i];
LL z = f[i];
if (d[y] || !z) {
continue;
}
q.push(y), d[y] = d[x] + 1;
if (y == T) {
return 1;
}
}
}
return 0;
}
LL dfs(LL x, LL now = INF) {
if (x == T) {
return now;
}
LL rst = now;
for (LL &i = hi[x]; i!=-1; i = ne[i]) {
LL y = e[i];
LL z = f[i];
if (d[y] != d[x] + 1 || !z) {
continue;
}
LL k = dfs(y, min(z, rst));
if (!k) {
d[y] = 0;
} else {
f[i] -= k, f[i^1] += k, rst -= k;
}
if (!rst) {
break;
}
}
return now - rst;
}
inline void main() {
while (bfs()) {
for (LL i = 1; i <= n; i++) {
hi[i] = h[i];
}
LL now;
while ((now = dfs(S))) {
mxf += now;
}
}
}
inline void init(LL _n, LL _S, LL _T) {
n = _n, S = _S, T = _T, idx = 0, mxf = 0;
for (LL i = 0; i <= n; i++) {
h[i] = -1;
}
}
}