8242: ABC278 —— E - Grid Filling
[Creator : ]
Description
You have a grid with H rows from top to bottom and W columns from left to right. We denote by (i,j) the square at the i-th row from the top and j-th column from the left. (i,j) (1≤i≤H,1≤j≤W) has an integer $A_{i,j}$ between 1 and N written on it.
You are given integers h and w. For all pairs (k,l) such that 0≤k≤H−h and 0≤l≤W−w, solve the following problem:
You are given integers h and w. For all pairs (k,l) such that 0≤k≤H−h and 0≤l≤W−w, solve the following problem:
- If you black out the squares (i,j) such that k<i≤k+h and l<j≤l+w, how many distinct integers are written on the squares that are not blacked out?
Input
The input is given from Standard Input in the following format:
$H\ W\ N\ h\ w$
$A_{1,1}\ A_{1,2}\ …\ A_{1,W}$
$A_{2,1}\ A_{2,2}\ …\ A_{2,W}$
$⋮$
$A_{H,1}\ A_{H,2}\ …\ A_{H,W}$
$H\ W\ N\ h\ w$
$A_{1,1}\ A_{1,2}\ …\ A_{1,W}$
$A_{2,1}\ A_{2,2}\ …\ A_{2,W}$
$⋮$
$A_{H,1}\ A_{H,2}\ …\ A_{H,W}$
Output
Print the answers in the following format, where ans_{k,l} denotes the answer to (k,l):
$\text{ans}_{0,0}\ \text{ans}_{0,1}\ … \text{ans}_{0,W−w}$
$\text{ans}_{1,0}\ \text{ans}_{1,1}\ … \text{ans}_{1,W−w}$
$⋮$
$\text{ans}_{H-h,0}\ \text{ans}_{H-h,1}\ … \text{ans}_{H-h,W−w}$
$\text{ans}_{0,0}\ \text{ans}_{0,1}\ … \text{ans}_{0,W−w}$
$\text{ans}_{1,0}\ \text{ans}_{1,1}\ … \text{ans}_{1,W−w}$
$⋮$
$\text{ans}_{H-h,0}\ \text{ans}_{H-h,1}\ … \text{ans}_{H-h,W−w}$
Constraints
$1≤H,W,N≤300$
$1≤h≤H$
$1≤w≤W$
$(h,w)\neq (H,W)$
$1≤A_{i,j}≤N\ (1≤i≤H,1≤j≤W)$
All values in the input are integers.
$1≤h≤H$
$1≤w≤W$
$(h,w)\neq (H,W)$
$1≤A_{i,j}≤N\ (1≤i≤H,1≤j≤W)$
All values in the input are integers.
Sample 1 Input
3 4 5 2 2
2 2 1 1
3 2 5 3
3 4 4 3
Sample 1 Output
4 4 3
5 3 4
The given grid is as follows:
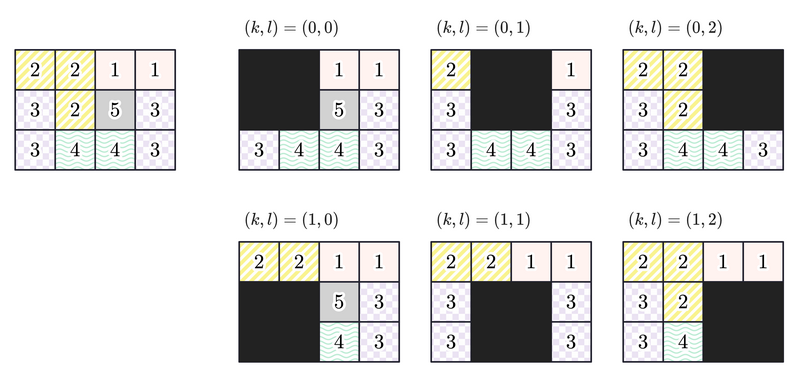
For example, when (k,l)=(0,0), four distinct integers 1,3,4, and 5 are written on the squares that are not blacked out, so 4 is the answer.

For example, when (k,l)=(0,0), four distinct integers 1,3,4, and 5 are written on the squares that are not blacked out, so 4 is the answer.
Sample 2 Input
5 6 9 3 4
7 1 5 3 9 5
4 5 4 5 1 2
6 1 6 2 9 7
4 7 1 5 8 8
3 4 3 3 5 3
Sample 2 Output
8 8 7
8 9 7
8 9 8
Sample 3 Input
9 12 30 4 7
2 2 2 2 2 2 2 2 2 2 2 2
2 2 20 20 2 2 5 9 10 9 9 23
2 29 29 29 29 29 28 28 26 26 26 15
2 29 29 29 29 29 25 25 26 26 26 15
2 29 29 29 29 29 25 25 8 25 15 15
2 18 18 18 18 1 27 27 25 25 16 16
2 19 22 1 1 1 7 3 7 7 7 7
2 19 22 22 6 6 21 21 21 7 7 7
2 19 22 22 22 22 21 21 21 24 24 24
Sample 3 Output
21 20 19 20 18 17
20 19 18 19 17 15
21 19 20 19 18 16
21 19 19 18 19 18
20 18 18 18 19 18
18 16 17 18 19 17