【作用】

树链剖分用于将树分割成若干条链的形式，以维护树上路径的信息。
具体来说，将整棵树剖分为若干条链，使它组合成线性结构，然后用其他的数据结构维护信息。

【性质】

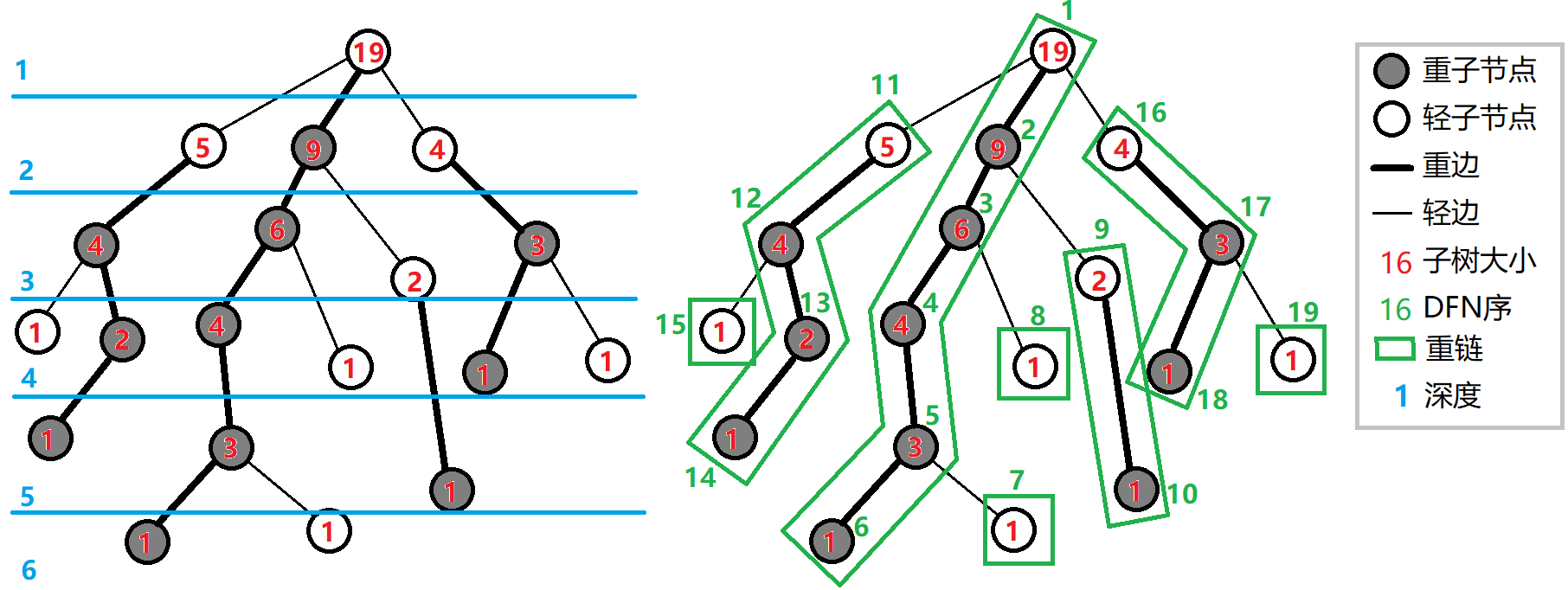
树上每个节点都属于且仅属于一条重链。
轻儿子一定是每条重链的顶点。
将树上的任意一条路径划分成不超过 $O(logn)$ $O(\log n)$ 条连续的链。

【概念】

重儿子：表示其子节点中子树最大的子结点。如果有多个子树最大的子结点，取其一。如果没有子节点，就无重子节点。
轻儿子：剩余的所有子结点。
重边：从这个结点到重子节点的边
轻边：到其他轻子节点的边
重链：若干条首尾衔接的重边构成

Input

【数据定义】

fa(x) 表示节点 x 在树上的父亲。
dep(x) 表示节点 x 在树上的深度。
siz(x) 表示节点 x 的子树的节点个数。
son(x) 表示节点 x 的 重儿子。
top(x) 表示节点 x 所在 重链 的顶部节点（深度最小）。
dfn(x) 表示节点 x 的 DFS 序，也是其在线段树中的编号。
rnk(x) 表示 DFS 序所对应的节点编号，有 rnk(dfn(x))=x。

【伪代码】

第一个 DFS 记录每个结点的父节点（fa）、深度（deep）、子树大小（size）、重子节点（hson）。

第二个 DFS 记录所在链的链顶（top，应初始化为结点本身）、重边优先遍历时的 DFS 序（dfn）、DFS 序对应的节点编号（rank）。

Output

【参考模板】

LL id[N];//id[x]为节点x的新编号
LL nw[N];//nw[x]是新编号为x的节点的权值
LL cnt;
LL deep[N];//deep[x]表示节点x的深度 
LL sz[N];//sz[x]表示以节点x为跟的子树节点数量 
LL top[N];//top[x]是x所在重链的头结点
LL fa[N];//fa[x]为x父亲
LL son[N];//son[x]为x的重儿子

//u:当前结点
//fath:u的父亲 
//求结点深度，父亲，子树大小，重儿子 
void dfs1(LL u,LL fath) {
	deep=deep[fath]+1;
	fa=fath;
	sz=1;
	
	for (LL i=h; i!=-1; i=ne[i]) {
		LL v=e[i];
		if (v==fath) {
			continue;
		}
		dfs1(v,u);
		//更新u
		sz+=sz[v];
		if (sz[son]<sz[v]) {
			//更新重儿子 
			son=v;
		}
	}
}

//u:当前结点
//t:u重链头结点 
void dfs2(LL u,LL t) {
	id=++cnt;
	nw[cnt]=w;//映射新权 
	top=t;
	if (0==son) {
		//u是叶子结点 
		return;
	}
	//先遍历重儿子 
	dfs2(son,t);
	//遍历轻儿子 
	for (LL i=h; i!=-1; i=ne[i]) {
		LL v=e[i];
		if (v==fa||v==son) {
			//v==fa返回到父亲结点
			//v==son是重儿子 
			continue;
		}
		dfs2(v,v);
	}
}

Constraints

【用途】

【使用树链剖分求 LCA】

【思路】
不断向上跳重链，当跳到同一条重链上时，深度较小的结点即为 LCA。
向上跳重链时需要先跳所在重链顶端深度较大的那个。
【时间复杂度】
$O(n+mlogn)$。
【代码】

LL lca(LL u,LL v) {
	while (top[u]!=top[v]) {
		if (deep[top[u]]<deep[top[v]]) {
			v=fa[top[v]];
		} else {
			u=fa[top[u]];
		}
	}
	return deep[u]<deep[v]?u:v;
}

【题目】
LCA。

【树上修改与查询问题】

【思路】
树链剖分 $\rightarrow$ 线段树维护 $\rightarrow$ 树上修改与查询。
通过树链剖分，剖分成为若干条重链，这样就可以转化成为一个有序序列。
我们可以使用线段树来维护这个有序序列，这样就将问题转换成为线段树区间修改和维护问题。
原树结构。

上图中，黑色数字表示原树节点编号，绿色边表示重链，红色的数字表示树链剖分的 DFS 序序号。这样，我们将原树转换成为如下图的有序序列。

利用线段树，我们将上图有序序列变成如下图的线段树。

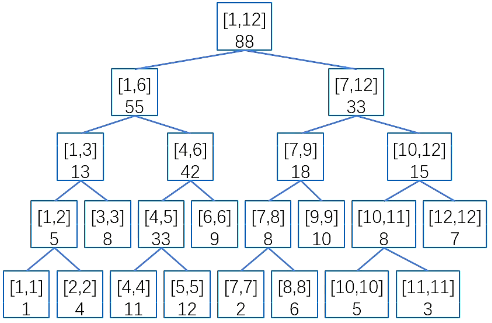
这样，我们将树上问题，转换成为线段树问题。
【时间复杂度】
$O(mlog^2n)$。其中 $m$ 表示查询次数， $n$ 表示节点数量。
【题目】
树链剖分。

8139: 学习系列 —— 树链剖分

Description