7993: ABC255 —— F - Pre-order and In-order
[Creator : ]
Description
Consider a binary tree with N vertices numbered 1,2,…,N. Here, a binary tree is a rooted tree where each vertex has at most two children. Specifically, each vertex in a binary tree has at most one left child and at most one right child.
Determine whether there exists a binary tree rooted at Vertex 1 satisfying the conditions below, and present such a tree if it exists.
Determine whether there exists a binary tree rooted at Vertex 1 satisfying the conditions below, and present such a tree if it exists.
Input
Input is given from Standard Input in the following format:
$N$
$P_1\ P_2\ …\ P_N$
$I_1\ I_2\ …\ I_N$
$N$
$P_1\ P_2\ …\ P_N$
$I_1\ I_2\ …\ I_N$
Output
If there is no binary tree rooted at Vertex 1 satisfying the conditions in Problem Statement, print -1.
Otherwise, print one such tree in N lines as follows. For each i=1,2,…,N, the i-th line should contain $L_i$ and $R_i$, the indices of the left and right children of Vertex i, respectively. Here, if Vertex i has no left (right) child, $L_i\ (R_i)$ should be 0.
If there are multiple binary trees rooted at Vertex 1 satisfying the conditions, any of them will be accepted.
$L_1\ R_1$
$L_2\ R_2$
$⋮$
$L_N\ R_N$
Otherwise, print one such tree in N lines as follows. For each i=1,2,…,N, the i-th line should contain $L_i$ and $R_i$, the indices of the left and right children of Vertex i, respectively. Here, if Vertex i has no left (right) child, $L_i\ (R_i)$ should be 0.
If there are multiple binary trees rooted at Vertex 1 satisfying the conditions, any of them will be accepted.
$L_1\ R_1$
$L_2\ R_2$
$⋮$
$L_N\ R_N$
Constraints
$2≤N≤2×10^5$
N is an integer.
$(P_1,P_2,…,P_N)$ is a permutation of (1,2,…,N).
$(I_1,I_2,…,I_N)$ is a permutation of (1,2,…,N).
N is an integer.
$(P_1,P_2,…,P_N)$ is a permutation of (1,2,…,N).
$(I_1,I_2,…,I_N)$ is a permutation of (1,2,…,N).
Sample 1 Input
6
1 3 5 6 4 2
3 5 1 4 6 2
Sample 1 Output
3 6
0 0
0 5
0 0
0 0
4 2
The binary tree rooted at Vertex 1 shown in the following image satisfies the conditions.
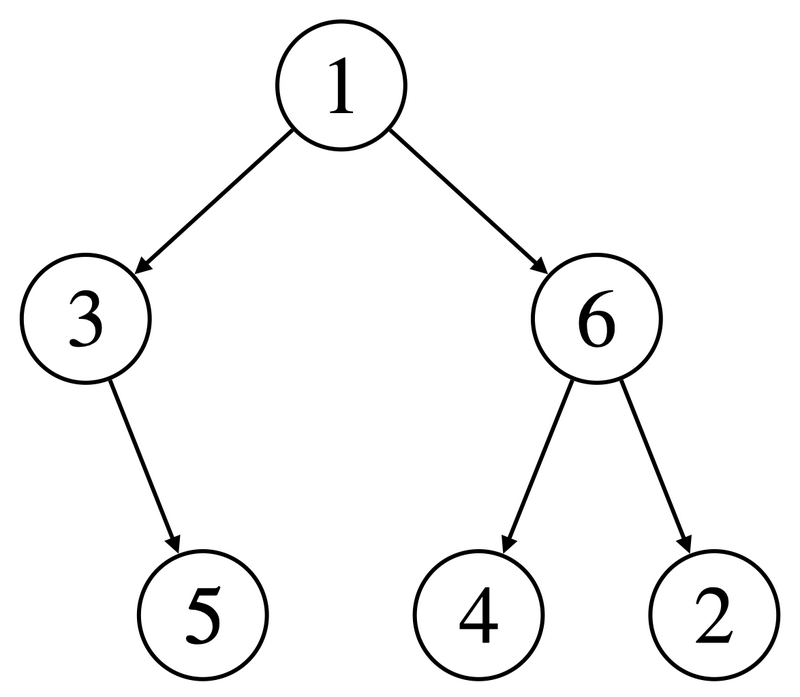
Sample 2 Input
2
2 1
1 2
Sample 2 Output
-1
No binary tree rooted at Vertex 1 satisfies the conditions, so −1 should be printed.