Description

【Tarjan 求 LCA】

Tarjan 发明了很多算法。
和倍增求 LCA 相比 Tarjan 算法是离线算法。离线算法，顾名思义，就是在一次遍历中把所有询问一次性解决，所以其时间复杂度是 $O(n+q)$。
如下图所示的树。

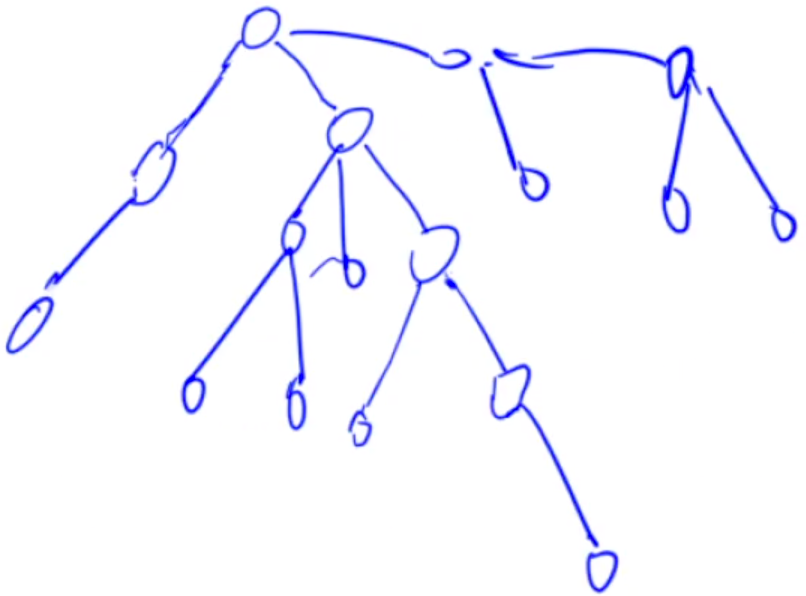
我们将当前搜索状态分为 $3$ 类。
$0$ 还没有搜索的分支；
$1$ 正在搜索的分支；
$2$ 已经遍历过，且回溯过。
如下图所示，绿色为 $2$，红色为 $1$，蓝色为 $0$。

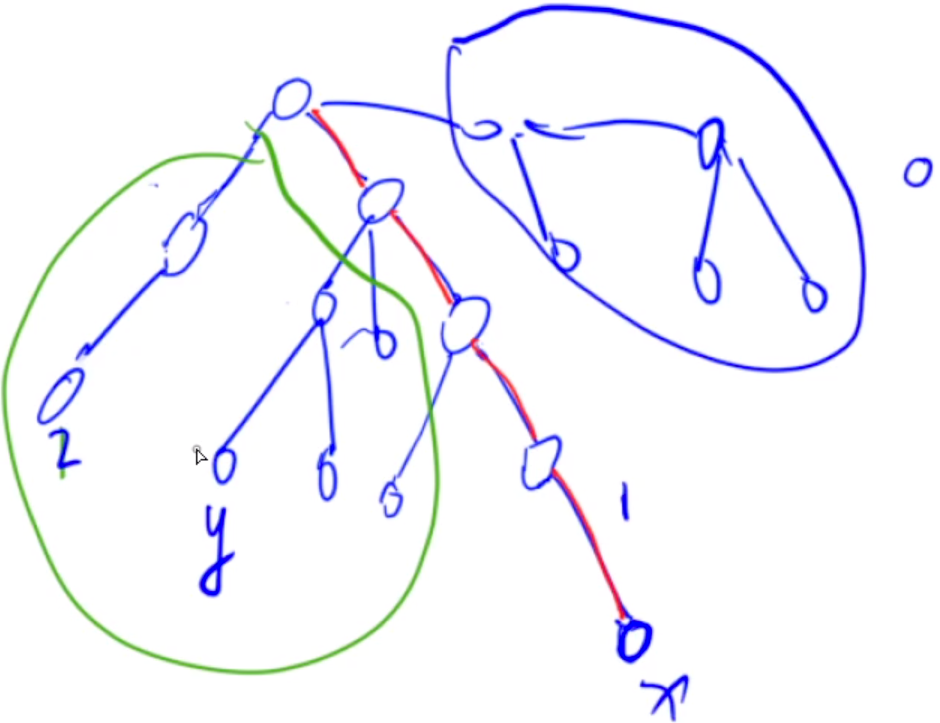
如上图所示，我们想知道正在搜索的节点红色 $x$ 和已经搜索过的节点绿色 $y$ 的最近公共祖先。我们只需要查询 $y$ 在并查集中的位置即可。

Tarjan算法的优点在于相对稳定，时间复杂度也比较居中，也很容易理解。
下面详细介绍一下Tarjan算法的基本思路：
1. 任选一个点为根节点，从根节点开始。
2. 遍历该点 $u$ 所有子节点 $v$，并标记这些子节点 $v$ 已被访问过。
3. 若是 $v$ 还有子节点，返回 2，否则下一步。
4. 合并 $v$ 到 $u$ 上。
5. 寻找与当前点 $u$ 有询问关系的点 $v$。
6. 若是 $v$ 已经被访问过了，则可以确认 $u$ 和 $v$ 的最近公共祖先为 $v$ 被合并到的父亲节点 $a$。

【时间复杂度】

$O(n+q)$，其中 $n$ 为顶点数，$q$ 是查询数量。

Input

【伪代码】

Tarjan(u)//marge和find为并查集合并函数和查找函数
{
    for each(u,v)    //访问所有u子节点v
    {
        Tarjan(v);        //继续往下遍历
        marge(u,v);    //合并v到u上
        标记v被访问过;
    }
    for each(u,e)    //访问所有和u有询问关系的e
    {
        如果e被访问过;
        u,e的最近公共祖先为find(e);
    }
}

Output

【数据结构】

//存储树
const int N=5e5+10;
LL h[N];
const int M=2*N;
LL e[M], w[M], ne[M], idx;
//并查集
LL fa[N];//编号为 i 的节点父亲是谁
//状态
LL st[N];//编号为 i 的节点状态
//st=0. 当前节点没有遍历过
//st=1.  当前节点正在遍历，没有被回溯
//st=2  当前节点被遍历过，且被回溯过
LL res[N];//编号为 i 的节点答案
LL dis[N];//编号为 i 的节点到跟节点的距离
const int Q=1e6+10;
vector<PLL> query[Q];//存储所有的查询 
LL n;//顶点的数量

【初始化】

for (LL i=0; i<=n; i++) {
    st[i]=0;//初始化状态
    fa[i]=i;//初始化并查集
    h[i]=-1;//初始化头节点
    dis[i]=0;//初始化距离 
    res[i]=0;
}
idx=0;
query.clear();

【预处理】
根据题目不同，进行预处理，比如下面的预处理，计算节点到跟节点距离

void dfs(LL u, LL fath)//求结点u到根节点的距离
{
    for (LL i=h; ~i; i=ne[i]) {
        LL v=e[i];
        if (v==fath) {
            continue;
        }
        dist[v]=dist+w[i];
        dfs(v, u);
    }
}

【tarjan算法】

void tarjan(LL u) {
    st=1;//表示当前点被遍历到
    
    for (LL i=h; ~i; i=ne[i]) {
        LL v=e[i];
        if (!st[v]) {
            tarjan(v);
            p[v]=u;//结点v的父节点为u
        }
    }
    
    for(auto item:query) {
        LL v=item.first, id=item.second;
        if (st[v]==2) {
            LL anc=find(v);//查找v的父亲
            res[id]=dist+dist[v]-2*dist[anc];
        }
    }
    
    st=2;//标志节点u为回溯完成
}

7749: 学习系列 —— 图论 —— 最近公共祖先 —— Tarjan算法