7747: 学习系列 —— 图论 —— 最近公共祖先 —— 倍增求 LCA
[Creator : ]
Description
【概念】
【最近公共祖先】
Lowest Common Ancestors (LCA) 。是指在有根树中,找出某两个结点 $u$ 和 $v$ 最近的公共祖先。在一棵没有环的树上,每个节点肯定有其父亲节点和祖先节点,而最近公共祖先,就是两个节点在这棵树上深度最大的公共的祖先节点。
换句话说,就是两个点在这棵树上距离最近的公共祖先节点。

如上图所示 4 和 5 的最近公共祖先是 2,5 和 3 的最近公共祖先是 1,2 和 1 的最近公共祖先是 1。
【问题】
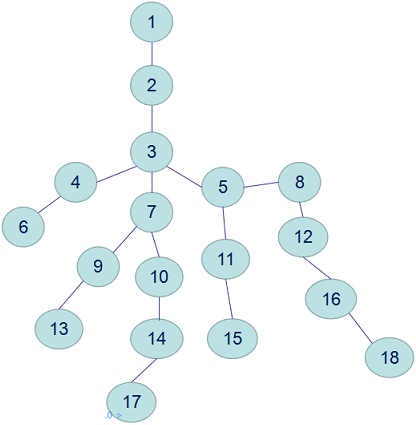
如上图的关系中,求 LCA。
【暴力算法】
以 $17$ 和 $18$ 为例,既然要求 LCA,那么我们就让他们一个一个向上爬,直到相遇为止。第一次相遇即是他们的LCA。模拟一下就是:
17->14->10->7->3
18->16->12->8->5->3
最终结果就是 $3$。
当然我们知道,这样的算法最终得到一个 TLE。
【倍增】
所谓倍增,就是按 $2$ 的倍数来增大,也就是跳 1,2,4,8,16,32……。不过在这我们不是按从小到大跳,而是从大向小跳,即按 ……32,16,8,4,2,1 来跳,如果大的跳不过去,再把它调小。这是因为从小开始跳,可能会出现“悔棋”的现象。拿 5 为例,从小向大跳,5≠1+2+4,所以我们还要回溯一步,然后才能得出5=1+4;而从大向小跳,直接可以得出5=4+1。
这也可以拿二进制为例,5(101),从高位向低位填很简单,如果填了这位之后比原数大了,那我就不填,这个过程是很好操作的。
同样这里以编号为 $17$ 和 $18$ 结点为例
17−>3
18−>5−>3
可以看出向上跳的次数大大减小。这个算法的时间复杂度为 $O(mlogn)$,已经可以满足大部分的需求。
【时间复杂度】
$O(mlogn)$,其中 $m$ 表示查询次数,$n$ 表示顶点数量。
Input
【fa 数组】

【倍增求 LCA】
【Step 1】
将 $v, w$ 跳到同一层。
如上图,deep[v]=10, deep[w]=1,所以我们知道两者深度差为 $10-1=9$,$9$ 对应的二进制为 $1001$,也就是说,先跳一次 $8$。

然后我们再跳 $1$ 步,就将 $v,w$ 变成同一层。


【Step 2】
将 $v,w$ 一起跳到 LCA 的下一层。现在,我们系统的结构如下图。

如上图所示。deep[v]=11,LCA 的下一层的 deep 为 $4$,因此 $11-4=7$,对应的二进制为 $111$。
第一次跳 $4$ 层。如下图。

第二次跳 $2$ 层,如下图。

第三次跳 $1$ 层,如下图。

这样,$v,w$ 的最近公共祖先就应该是 fa[v][0],即然 $v$ 再跳 $2^0=1$ 步即可。
Output
【倍增求 LCA】
倍增求 LCA 是一种在线算法。想要实现这个算法,首先我们要记录各个点的深度和他们 $2^i$ 级的的祖先,用数组 deep 表示每个节点的深度,fa[i][j] 表示节点 $i$ 的 $2^j$ 级祖先。
【数据保存】
使用数组。和图论使用邻接表存图的方法一样。//存图 const int M=2e6+10; LL e[M], ne[M], idx; //LCA数据 const int N=5e5+10; LL h[N];//头节点 LL deep[N];//编号为i的节点深度 LL dis[N];//编号为i的节点到跟节点距离 LL fa[N][30+2];//节点i的2^j级祖先
【预处理】
BFSvoid bfs(LL st) {
queue<LL> que;
que.push(st);
deep[st]=1;
while (que.size()) {
LL u=q.front();
q.pop();
for(int i=h; i!=-1; i=ne[i]) {
LL v=e[i];
if (deep[v]) {
continue;
}
deep[v]=deep[v]+1;
fa[v][0]=u;
for(LL j=1; j<=30;j++) {
f[v][j]=f[f[v][j-1]][j-1];
}
q.push(v);
}
}
}
DFS
//u表示当前节点,
//fath表示它的父亲节点
void dfs(LL now, LL fath) {
fa[0]=fath;//更新当前x的爸爸,即2^0=1代祖宗
deep = deep[fath]+1;//孩子是爹的深度+1
for (LL i=1; (1<<i)<=deep; i++) {
fa[i]=fa[fa[i-1]][i-1];//这个转移可以说是算法的核心之一
//意思是f的2^i祖先等于f的2^(i-1)祖先的2^(i-1)祖先
//2^i=2^(i-1)+2^(i-1)
}
for(int i=h; i!=-1; i=ne[i]) {
LL v=e[i];
if (v!=fath) {
dfs(v,u);
}
}
}
【求 LCA】
LL lca(LL x,LL y){
if (deep[x]<deep[y]) {
swap(x,y);//令x为深度较深的结点
}
for (LL i=30; i>=0; i--) {
if(dep[fa[x][i]]>=dep[y]) {
x=fa[x][i];//若x的2^i级爸爸的深度大于等于y的深度,更新x
}
}
if (x==y) {
return x;//特判,x的爸爸就是y
}
for (LL i=30; i>=0; i--) {
if (fa[x][i]!=fa[y][i]) {
x=fa[x][i];
y=fa[y][i];//若x和y的爸爸不相同,同时往上跳直到找到x和y的共同爸爸
}
}
return fa[x][0];//返回x的爸爸
}