【概念】

【欧拉路（Eulerian Path（or Eulerian Trail））】

给定无孤立结点图G，若存在一条路，经过图中每条边一次且仅一次，该条路为欧拉路。

其中 1 -> 2 -> 3 -> 5 -> 10 -> 3 -> 4 -> 8 -> 9 -> 11 -> 8 -> 7 -> 6 就是一条欧拉路。
当然 1 -> 2 -> 3 -> 10 -> 5 -> 3 -> 4 -> 8 -> 11 -> 9 -> 8 -> 7 -> 6 也是一条欧拉路。
然后 6 -> 7 -> 8 -> 11 -> 9 -> 8 -> 4 -> 3 -> 10 -> 5 -> 3 -> 2 -> 1 所以反过来还是欧拉路。
由此可以看出，一个图的欧拉路并不是唯一的。

【欧拉回路（Eulerian Circuit）】

若存在一条回路，经过图中每边一次且仅一次，该回路称为欧拉回路。

如上图所示，我们只需要在 1 和 6 中间加上一条边，就存在一条欧拉回路。

	Eulerian Circuit	Eulerian Path
无向图	每个顶点的度数都是偶数	每个顶点的度数是偶数。 或者只能有两个顶点的度数为奇数，这两个顶点为起点和终点。
有向图	每个顶点的入度和出度相同	最多一个顶点 $d_{out}-d_{in}=1$ 最多一个顶点 $d_{in}-d_{out}=1$ 其他顶点的入度和出度相同

求解算法

1.1 DFS遍历寻找欧拉路

设给定一张图，已知这张图是欧拉路，要求输出整条欧拉路。
此时可以采用 DFS 来遍历整张图，寻找欧拉路。使用 DFS 寻找欧拉路的基本思想如下：
1. DFS寻找到第一个无边可走的节点，则这个节点必定为终点。
2. 接下来由于DFS的递归回溯，会退回终点的上一个节点，继续往下搜索，直到寻找到第二个无边可走的节点，则这个节点必定为欧拉路中终点前最后访问的节点。
3. 于是当通过DFS遍历完整张图后，就可以倒序储存下整个欧拉路。
为了便于理解，我们举个例子来进行讲解：

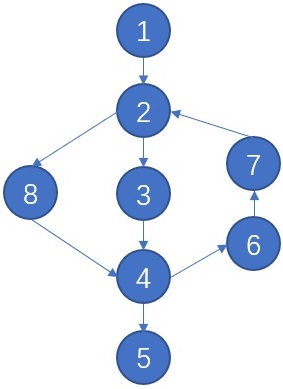
在上图中，存在一个欧拉路。假设我们 DFS 时以 1 为起点，优先访问编号小的节点。
则我们将访问 1-2-3-4-5，直到 5 节点时，无边可访问，则将 5 记录进答案中。
接着回溯，继续访问 6-7-2-8-4。此时所有边已经全部访问，那就根据DFS的过程将节点一一存储进答案。此时的答案数组为 5-4-8-2-7-6-4-3-2-1。
我们可以发现，这就是欧拉路遍历节点的逆序过程。将答案数组逆序输出，即可求出欧拉路。