Description

知识点

非递归线段树，因为张昆玮在统计的力量中介绍了这种数据结构，常常被称为zkw线段树，是一种代码较短、常数较小的线段树写法。
普通的线段树，是从上到下处理的。因为对于普通线段树，我们很容易定位根节点，却不容易定位叶子节点。

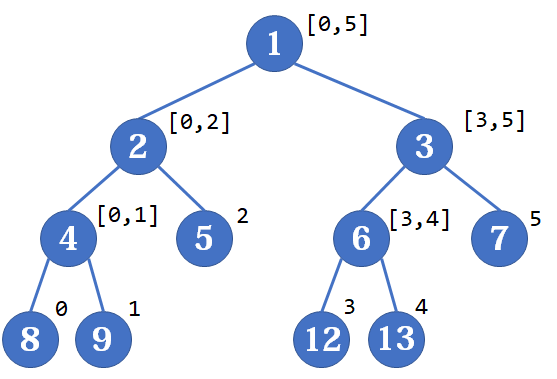
为了后面方便，本文统一对节点采用 1-index，对线段采用 0-index。
但是，一种特殊情况下，线段树的叶子节点很好定位，那就是这棵二叉树是满二叉树时：

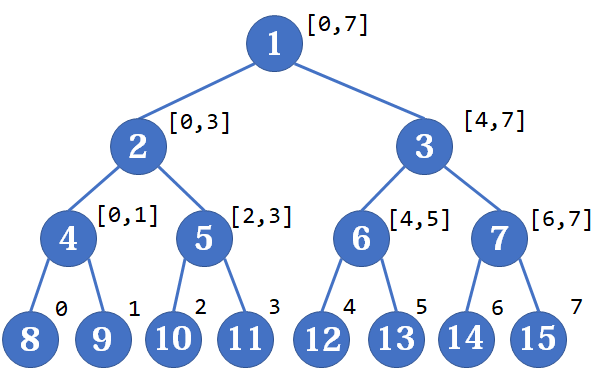
这时我们发现叶子节点的编号非常有规律，设一共有 n 个叶子节点，若某叶子节点所代表的退化线段为 [x,x] ，则其编号 p=x+n 。不仅如此，这棵树还有大量很好的性质：

整棵树一共有 2n−1 个节点
一共有 $H=log_2⁡(n)+1$ 层，（从上往下数）第 h 层有 $2^{h−1}$ 个节点，且该层线段长度为 $2^{H−h}$
若某节点的编号为 p ，其父节点编号为 ⌊p/2⌋ ，子节点编号为 2p 和 2p+1 。
若两节点编号分别为 p 和 q ，则它们是兄弟节点等价于 p⊕q=1 。
除根结点外，编号为偶数的节点都是某个节点的左节点，编号为奇数的节点都是某个节点的右节点。

要构建出这样一棵满二叉树，需要让 n 是 2 的整数幂。如果 n 不是 2 的整数幂怎么办呢？很简单，往后补 0 使它成为 2 的整数幂即可。

Input

建树

以维护和信息为例

int N = 1 << __lg(n + 5) + 1;
vector<int> tree(N << 1);
for (int i = 1; i <= n ++i)
    tree[i + N] = A[i];
for (int i = N; i; --i)
    tree[i] = tree[i << 1] + tree[i << 1 | 1];

单点修改

void update(int x, int d) {
    for (int i = x + N; i; i >>= 1) 
        tree[i] += d;
}

区间查询

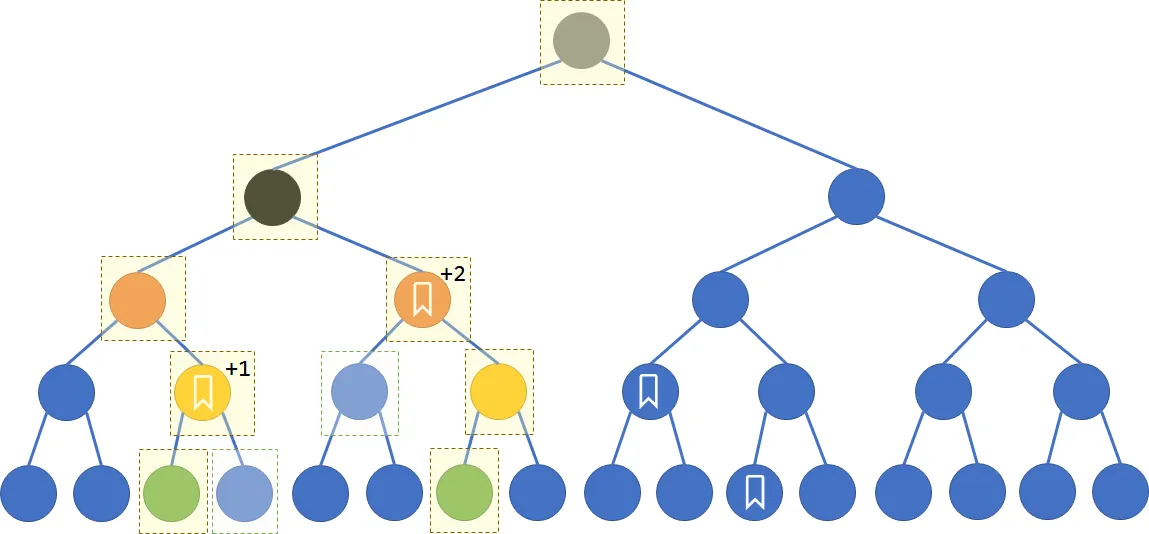
我们把查询 [l,r] 这个闭区间的信息换成查询 (l−1,r+1) 这个开区间的信息。然后从下往上，一层一层地缩小区间范围。

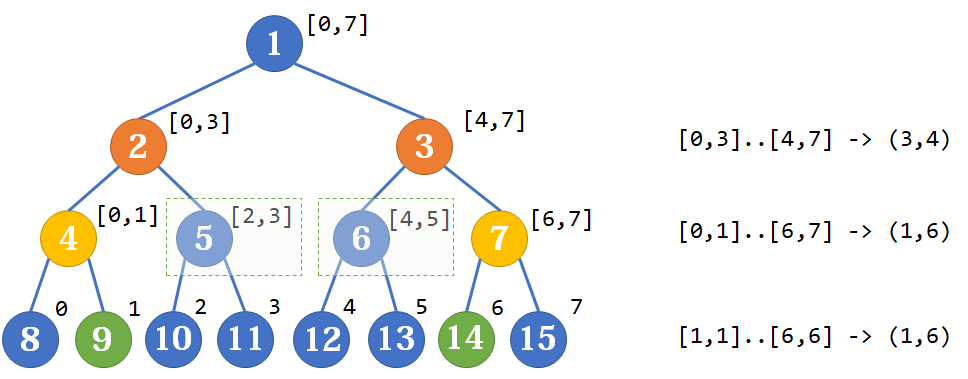
观察上图发现，不断上移的过程，就是不断把端点及其兄弟排除出查询区间的过程。而如果查询区间的左端点是父节点的左儿子 / 右端点是父节点的右儿子，说明它的兄弟应当是答案的一部分。最后在查询的区间为空区间（两端点为兄弟节点）时，退出循环。

int query(int l, int r) {
    int ans = 0;
    for (l += N - 1, r += N + 1; l ^ r ^ 1; l >>= 1, r >>= 1) {
        if (~l & 1) ans += tree[l ^ 1]; // 左端点是左儿子
        if (r & 1) ans += tree[r ^ 1]; // 右端点是右儿子
    }
    return ans;
}

区间修改

稍微麻烦一点点。在非递归的情况下，标记下传是比较困难的，所以我们不下传标记，而是将标记永久化。
具体地，和上文中区间查询类似，当左端点是左儿子/右端点是右儿子时，我们对它的兄弟进行修改并打上标记，表示这棵子树中每个节点都要修改。但单纯这样是不够的，因为上述修改还会波及到这些节点的各级祖先。所以我们需要在途中根据实际修改的区间长度来更新各级祖先的值，而且这种操作需要一路上推到根节点。

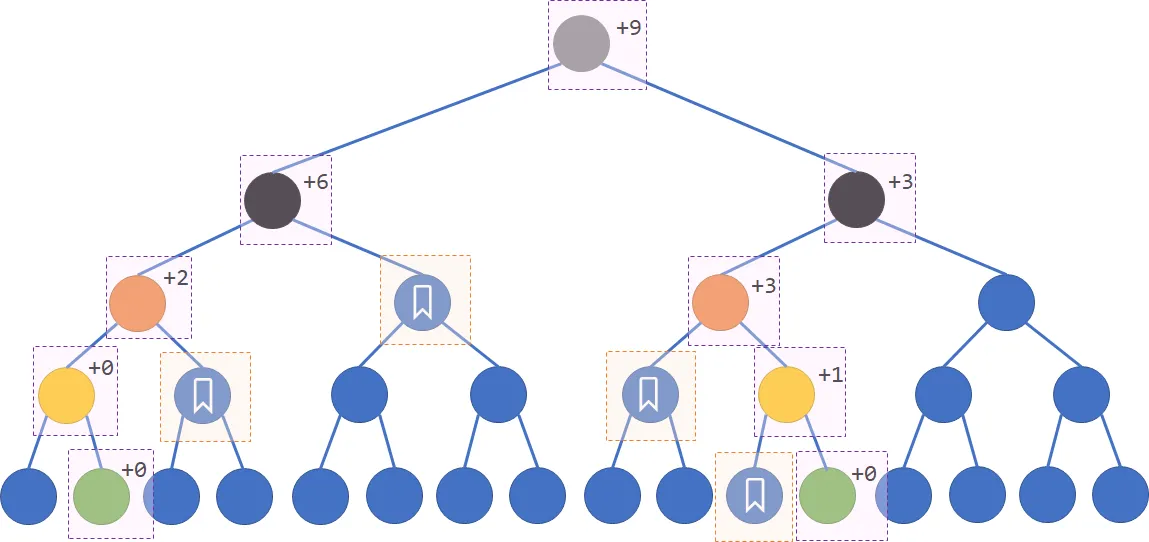
void update(int l, int r, int d) {
    int len = 1, cntl = 0, cntr = 0; // cntl、cntr是左、右两边分别实际修改的区间长度
    for (l += N - 1, r += N + 1; l ^ r ^ 1; l >>= 1, r >>= 1, len <<= 1) {
        tree[l] += cntl * d, tree[r] += cntr * d;
        if (~l & 1) tree[l ^ 1] += d * len, mark[l ^ 1] += d, cntl += len;
        if (r & 1) tree[r ^ 1] += d * len, mark[r ^ 1] += d, cntr += len;
    }
    for (; l; l >>= 1, r >>= 1)
        tree[l] += cntl * d, tree[r] += cntr * d;
}

在有区间修改存在时，区间查询也需要考虑标记的影响。所以除了加上端点的兄弟节点的信息，沿途中遇到的标记也对答案有相应的贡献，依赖于实际查询的区间长度，这同样也需要上推到根节点。

int query(int l, int r) {
    int ans = 0, len = 1, cntl = 0, cntr = 0;
    for (l += N - 1, r += N + 1; l ^ r ^ 1; l >>= 1, r >>= 1, len <<= 1) {
        ans += cntl * mark[l] + cntr * mark[r];
        if (~l & 1) ans += tree[l ^ 1], cntl += len;
        if (r & 1) ans += tree[r ^ 1], cntr += len;
    }
    for (; l; l >>= 1, r >>= 1)
        ans += cntl * mark[l] + cntr * mark[r];
    return ans;
}

Output

再补充一个区间加、区间查询最大值的模板：

void update(int l, int r, int d) {
    for (l += N - 1, r += N + 1; l ^ r ^ 1; l >>= 1, r >>= 1)
    {
        if (l < N) tree[l] = max(tree[l << 1], tree[l << 1 | 1]) + mark[l],
                    tree[r] = max(tree[r << 1], tree[r << 1 | 1]) + mark[r];
        if (~l & 1) tree[l ^ 1] += d, mark[l ^ 1] += d;
        if (r & 1) tree[r ^ 1] += d, mark[r ^ 1] += d;
    }
    for (; l; l >>= 1, r >>= 1)
        if (l < N) tree[l] = max(tree[l << 1], tree[l << 1 | 1]) + mark[l],
                    tree[r] = max(tree[r << 1], tree[r << 1 | 1]) + mark[r];
}
int query(int l, int r) {
    int maxl = -INF, maxr = -INF;
    for (l += N - 1, r += N + 1; l ^ r ^ 1; l >>= 1, r >>= 1)
    {
        maxl += mark[l], maxr += mark[r];
        if (~l & 1) cmax(maxl, tree[l ^ 1]);
        if (r & 1) cmax(maxr, tree[r ^ 1]);
    }
    for (; l; l >>= 1, r >>= 1)
        maxl += mark[l], maxr += mark[r];
    return max(maxl, maxr);
}

7441: 学习系列 —— 线段树 —— zkw线段树