概念

差分约束系统，system of difference constraints，是求解关于一组变数的特殊不等式组之方法。如果一个系统由 $n$ 个变量和 $m$ 个约束条件组成，其中每个约束条件形如 $x_j - x_i \leq b_k\ (i,j \in [1,n],\ k \in [1,m])$，则称其为差分约束系统，system of difference constraints。亦即，差分约束系统是求解关于一组变量的特殊不等式组的方法。
差分约束系统是下面这种形式的多元一次不等式组，$y_1, y_2, \cdots,y_n$ 为已知量：
$\begin{equation} \begin{cases}x_{c_1}-x_{c_{1^{'}}} \leq y_1 \\ x_{c_2}-x_{c_{2^{'}}} \leq y_2 \\ \cdots \\ x_{c_n}-x_{c_{n^{'}}}\leq y_n \end{cases} \end{equation}$

每个不等式称为一个约束条件，都是两个未知量之差小于或等于某个常数。
在算法竞赛中，很多题目会给出（或隐性地给出）一系列的不等关系，我们可以尝试把它们转化为差分约束系统来解决。

解法

我们设 $x_1−x_2≤c$ ，移项得 $x_1≤x_2+c$。说明 $x_2$ 经过一条权为 $c$ 的有向路到达 $x_1$，也就是有一条 $x_2 \to x_1$ 权为 $c$ 的有向边。
观察这个不等式与最短路问题中的三角形不等式 $dist≤dist[v]+w_{v,u}$ 的相似之处。利用这一点，我们可以把它转化为一个图论问题。也就是说，对于每一个 $x_{c_i}−x_{c_i^{'}}≤y_i$ ，我们都从 $c_i^{'}$ 到 $c_i$ 建一条边，边权为 $y_i$。
这样建出的有向图，它的每个顶点都对应差分约束系统中的一个未知量，源点到每个顶点的最短路对应这些未知量的值，而每条边对应一个约束条件。

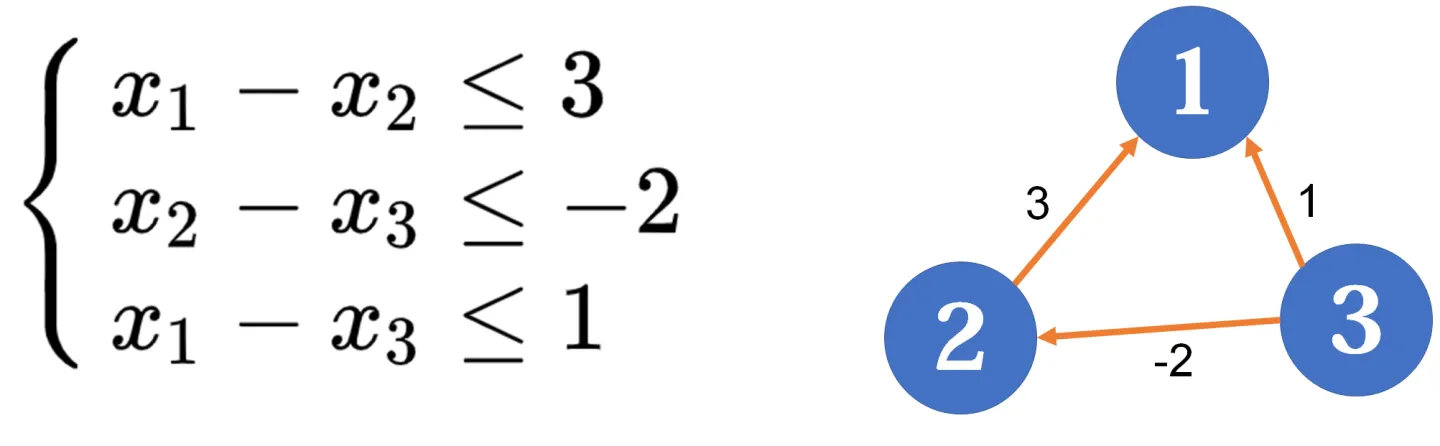
那么问题来了，既然是最短路，源点在哪里呢？
实际上取哪个点为源点是无关紧要的，但是，有时候我们得到的图不是连通的，这样求出来的结果很容易出现 INF。为了避免这种情形，我们习惯人为地增加一个超级源点。
例如我们现在人为地新增一个 0 号点（或 n+1 号点），从它向所有顶点连一条边权为 0 的边：

现在我们以 0 号点为源点求各点的最短路即可。注意，这相当于了添加了以下约束条件：
$\begin{equation} \begin{cases} x_{1}-x_{0} \leq 0\\ x_{2}-x_{0} \leq 0\\ x_{3}-x_{0}\leq 0 \end{cases} \end{equation}$
由于 $x_0$ 对应的是 dist[0]，而 dist[0]=0 ，可知所有未知量均小于等于 0（反映在图形上是所有点的最短路均小于等于 0）。这是为什么？实际上我们往往要的是非负解呀。
因为这求出的只是一组解，通过简单的数学计算可知，在符合差分约束系统的一组解上加上或减去同一个数，得到的解同样符合原系统。例如，上文例子求得的结果为 $x_1=0,\ x_2=−2,\ x_3=0$，然而 $x_1=2,\ x_2=0,\ x_3=2$ 也是一组解。
其实我们可以把 dist[0] 设为另一个数 w 而不是0，或者把从 0 号点连向各点的边权设为 w，那么我们得到的便是满足 $x_1, x_2, ..., x_n≤w$ 的一组解。实际上，可以证明，它们是满足 $x_1, x_2, ..., x_n≤w$ 的最大解，每个变量取到能取到的最大值。
那么如何求满足 $x_1, x_2, ..., x_n≥w$ 的最小解呢？只需要求最长路就行了。最长路满足三角形不等式 $dist≥dist[v]+w_{v,u}$，所以相应的差分约束系统需要把小于等于符号换成大于等于符号。
对于 Bellman-Ford 或 SPFA 算法来说，只需要初始化为 -INF 而不是 INF，然后把比较符号颠倒一下即可。

7435: 学习系列 —— 图论 —— 差分约束

Description

概念

解法

Input

Source/Category