7279: AtCoder Educational DP Contest —— G - Longest Path
[Creator : ]
Description
There is a directed graph G with $N$ vertices and $M$ edges.
The vertices are numbered $1,2,…,N$, and for each $i\ (1≤i≤M)$, the $i$-th directed edge goes from Vertex $x_i$ to $y_i$. $G$ does not contain directed cycles.
Find the length of the longest directed path in G. Here, the length of a directed path is the number of edges in it.
The vertices are numbered $1,2,…,N$, and for each $i\ (1≤i≤M)$, the $i$-th directed edge goes from Vertex $x_i$ to $y_i$. $G$ does not contain directed cycles.
Find the length of the longest directed path in G. Here, the length of a directed path is the number of edges in it.
Input
Input is given from Standard Input in the following format:
$N\ M$
$x_1\ y_1$
$x_2\ y_2$
$\vdots$
$x_M\ y_M$
$N\ M$
$x_1\ y_1$
$x_2\ y_2$
$\vdots$
$x_M\ y_M$
Output
Print the length of the longest directed path in G.
Constraints
All values in input are integers.
$2 \leq N \leq 10^5$
$1 \leq M \leq 10^5$
$1 \leq x_i, y_i \leq N$
All pairs $(x_i, y_i)$ are distinct.
G does not contain directed cycles.
$2 \leq N \leq 10^5$
$1 \leq M \leq 10^5$
$1 \leq x_i, y_i \leq N$
All pairs $(x_i, y_i)$ are distinct.
G does not contain directed cycles.
Sample 1 Input
4 5
1 2
1 3
3 2
2 4
3 4
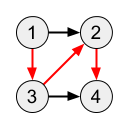
Sample 1 Output
3
The red directed path in the following figure is the longest:

Sample 2 Input
6 3
2 3
4 5
5 6
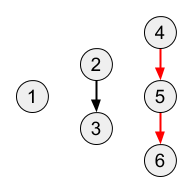
Sample 2 Output
2
The red directed path in the following figure is the longest:

Sample 3 Input
5 8
5 3
2 3
2 4
5 2
5 1
1 4
4 3
1 3
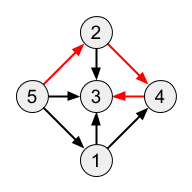
Sample 3 Output
3
The red directed path in the following figure is one of the longest: