You are given a sequence $A = (A_1, A_2, \dots, A_N)$ of length N consisting of positive integers, and integers x and y.
Determine whether it is possible to place N+1 points $p_1, p_2, \dots, p_N, p_{N+1}$ in the xy-coordinate plane to satisfy all of the following conditions. (It is allowed to place two or more points at the same coordinates.)

• $p_1 = (0, 0)$.
• $p_2 = (A_1, 0)$.
• $p_{N+1} = (x, y)$.
• The distance between the points $p_i$ and $p_{i+1}$ is $A_i$. (1≤i≤N)
• The segments $p_i p_{i+1}$ and $p_{i+1} p_{i+2}$ form a 90 degree angle. (1≤i≤N−1)

The input is given from Standard Input in the following format:
$N\ x\ y$
$A_1\ A_2\ \dots\ A_N$

If it is possible to place $p_1, p_2, \dots, p_N, p_{N+1}$ to satisfy all of the conditions in the Problem Statement, print Yes; otherwise, print No.

If it is possible to place $p_1, p_2, \dots, p_N, p_{N+1}$ to satisfy all of the conditions in the Problem Statement, print Yes; otherwise, print No.

Yes

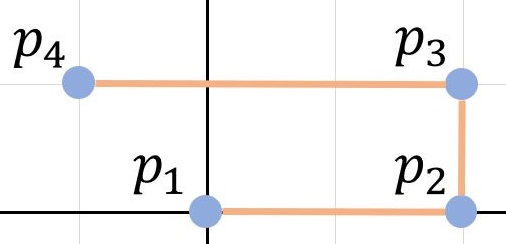
The figure below shows a placement where $p_1 = (0, 0), p_2 = (2, 0), p_3 = (2, 1)$, and $p_4 = (-1, 1)$. All conditions in the Problem Statement are satisfied.

Yes

Letting $p_1 = (0, 0), p_2 = (2, 0), p_3 = (2, 2), p_4 = (0, 2), p_5 = (0, 0)$, and $p_6 = (2, 0)$ satisfies all the conditions. Note that multiple points may be placed at the same coordinates.