Problem7183--ABC223 —— E - Placing Rectangles

7183: ABC223 —— E - Placing Rectangles

[Creator : ]
Time Limit : 1.000 sec  Memory Limit : 256 MiB

SubmitSolved: 1Submit Num: 1StatisticsShowOff!

Description

For positive integers X and Y, a rectangle in a two-dimensional plane that satisfies the conditions below is said to be good.
  • Every edge is parallel to the x- or y-axis.
  • For every vertex, its x-coordinate is an integer between 0 and X (inclusive), and y-coordinate is an integer between 0 and Y (inclusive).
Determine whether it is possible to place the following three good rectangles without overlapping: a good rectangle of an area at least A, another of an area at least B, and another of an area at least C.
Here, three rectangles are considered to be non-overlapping when the intersection of any two of them has an area of 0.

Input

Input is given from Standard Input in the following format:
$X\ Y\ A\ B\ C$

Output

If it is possible to place three rectangles under the conditions specified in the Problem Statement, print Yes; otherwise, print No.

Constraints

$1≤X,Y≤10^9$
$1 \leq A, B, C \leq 10^{18}$
All values in input are integers.

Sample 1 Input 

3 3 2 2 3

Sample 1 Output 

Yes

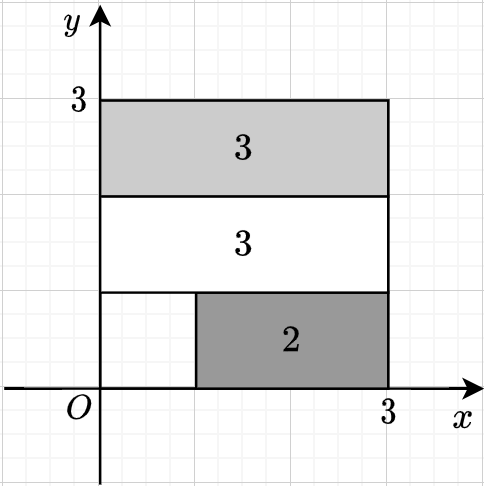
The figure below shows a possible placement, where the number in a rectangle represents its area.

We can see that $2 \geq A, 3 \geq B, 3 \geq C$, satisfying the conditions.

Sample 2 Input 

3 3 4 4 1

Sample 2 Output 

No
There is no possible placement under the conditions.

Sample 3 Input 

1000000000 1000000000 1000000000000000000 1000000000000000000 1000000000000000000

Sample 3 Output 

No

Source/Category

 
Submit