7168: ABC251 —— G - Intersection of Polygons
[Creator : ]
Description
The vertices of a convex $N$-gon $P$ in an xy-plane are given as $(x_1, y_1), (x_2, y_2), \ldots, (x_N, y_N)$ in the counterclockwise order. (Here, the positive direction of the x-axis is right, and the positive direction of the y-axis is up.)
Based on this polygon $P$, we consider $M$ convex $N$-gons $P_1, P_2, \ldots, P_M$.
For $i = 1, 2, \ldots, M$, the polygon $P_i$ is obtained by shifting $P$ in the positive direction of the x-axis by $u_i$ and in the positive direction of the y-axis by $v_i$. In other words, $P_i$ is a convex $N$-gon whose vertices are $(x_1+u_i, y_1+v_i), (x_2+u_i, y_2+v_i), \ldots, (x_N+u_i, y_N+v_i)$.
For each of $Q$ points $(a_1, b_1), (a_2, b_2), \ldots, (a_Q, b_Q)$, determine if "the point is contained in all of the $M$ polygons $P_1, P_2, \ldots, P_M$."
Here, we regard a point is also contained in a polygon if the point is on the polygon's boundary.
Based on this polygon $P$, we consider $M$ convex $N$-gons $P_1, P_2, \ldots, P_M$.
For $i = 1, 2, \ldots, M$, the polygon $P_i$ is obtained by shifting $P$ in the positive direction of the x-axis by $u_i$ and in the positive direction of the y-axis by $v_i$. In other words, $P_i$ is a convex $N$-gon whose vertices are $(x_1+u_i, y_1+v_i), (x_2+u_i, y_2+v_i), \ldots, (x_N+u_i, y_N+v_i)$.
For each of $Q$ points $(a_1, b_1), (a_2, b_2), \ldots, (a_Q, b_Q)$, determine if "the point is contained in all of the $M$ polygons $P_1, P_2, \ldots, P_M$."
Here, we regard a point is also contained in a polygon if the point is on the polygon's boundary.
Input
Input is given from Standard Input in the following format:
$N$
$x_1\ y_1$
$x_2\ y_2$
$\vdots$
$x_N\ y_N$
$M$
$u_1\ v_1$
$u_2\ v_2$
$\vdots$
$u_M\ v_M$
$Q$
$a_1\ b_1$
$a_2\ b_2$
$\vdots$
$a_Q\ b_Q$
$N$
$x_1\ y_1$
$x_2\ y_2$
$\vdots$
$x_N\ y_N$
$M$
$u_1\ v_1$
$u_2\ v_2$
$\vdots$
$u_M\ v_M$
$Q$
$a_1\ b_1$
$a_2\ b_2$
$\vdots$
$a_Q\ b_Q$
Output
Print $Q$ lines. For $i = 1, 2, \ldots, Q$, the $i$-th line should contain Yes if point $(a_i, b_i)$ is contained in all of the $M$ polygons $P_1, P_2, \ldots, P_M$; it should contain No otherwise.
Constraints
$3≤N≤50$
$1 \leq M \leq 2 \times 10^5$
$1 \leq Q \leq 2 \times 10^5$
$-10^8 \leq x_i, y_i \leq 10^8$
$-10^8 \leq u_i, v_i \leq 10^8$
$-10^8 \leq a_i, b_i \leq 10^8$
All values in input are integers.
$(x_1, y_1), (x_2, y_2), \ldots, (x_N, y_N)$ forms a convex $N$-gon in the counterclockwise order.
Each interior angle of the polygon $P$ is less than $180$ degrees.
$1 \leq M \leq 2 \times 10^5$
$1 \leq Q \leq 2 \times 10^5$
$-10^8 \leq x_i, y_i \leq 10^8$
$-10^8 \leq u_i, v_i \leq 10^8$
$-10^8 \leq a_i, b_i \leq 10^8$
All values in input are integers.
$(x_1, y_1), (x_2, y_2), \ldots, (x_N, y_N)$ forms a convex $N$-gon in the counterclockwise order.
Each interior angle of the polygon $P$ is less than $180$ degrees.
Sample 1 Input
5
-2 -3
0 -2
1 0
0 2
-2 1
2
0 1
1 0
6
0 0
1 0
0 1
1 1
-1 -1
-1 -2
Sample 1 Output
Yes
No
Yes
Yes
Yes
No
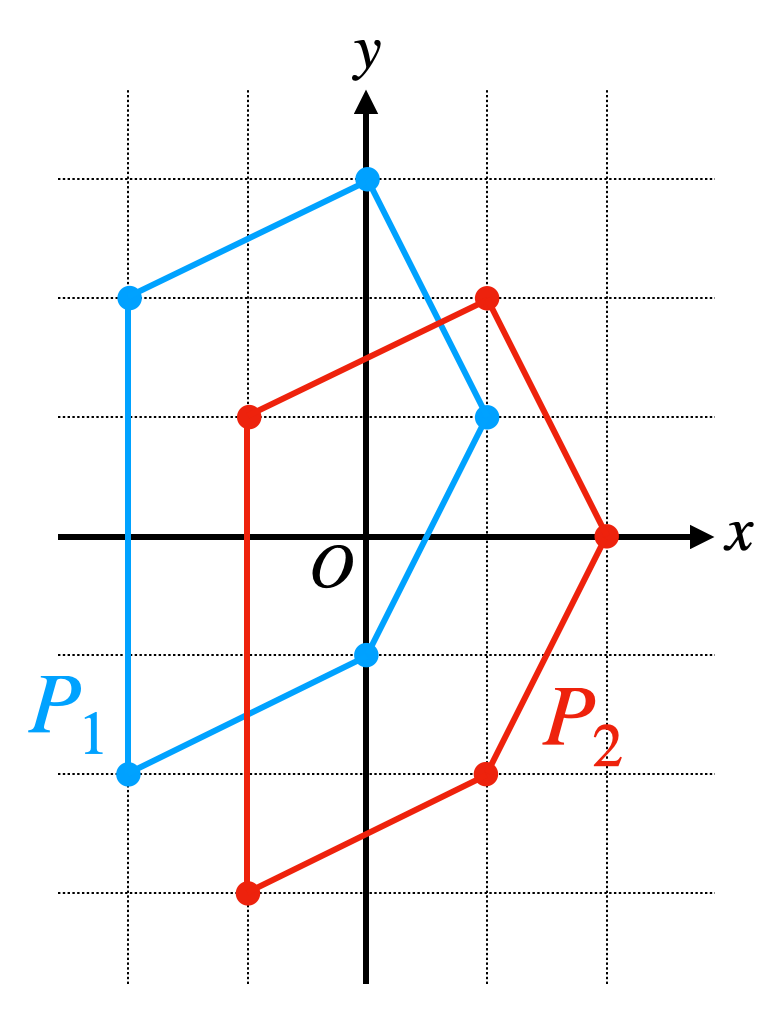
Polygon P is a pentagon (5-gon) whose vertices are (-2, -3), (0, -2), (1, 0), (0, 2), (-2, 1).
- Polygon $P_1 is a pentagon (5-gon) obtained by shifting P in the positive direction of the x-axis by 0 and in the positive direction of the y-axis by 1, so its vertices are (-2, -2), (0, -1), (1, 1), (0, 3), (-2, 2).
- Polygon $P_2$ is a pentagon (5-gon) obtained by shifting P in the positive direction of the x-axis by 1 and in the positive direction of the y-axis by 0, so its vertices are (-1, -3), (1, -2), (2, 0), (1, 2), (-1, 1).
Thus, the following 6 lines should be printed.
- The 1-st line should be Yes because $(a_1, b_1) = (0, 0)$ is contained in both $P_1$ and $P_2$.
- The 2-nd line should be No because $(a_2, b_2) = (1, 0)$ is contained in $P_2$ but not in $P_1$.
- The 3-rd line should be Yes because $(a_3, b_3) = (0, 1)$ is contained in both $P_1$ and $P_2$.
- The 4-th line should be Yes because $(a_4, b_4) = (1, 1)$ is contained in both $P_1$ and $P_2$.
- The 5-th line should be Yes because $(a_5, b_5) = (-1, -1)$ is contained in both $P_1$ and $P_2$.
- The 6-th line should be No because $(a_6, b_6) = (-1, -2)$ is contained in $P_2$ but not in $P_1$.
Note that a point on the boundary of a polygon is also considered to be contained in the polygon.
Sample 2 Input
10
45 100
-60 98
-95 62
-95 28
-78 -41
-54 -92
-8 -99
87 -94
98 23
87 91
5
-57 -40
-21 -67
25 39
-30 25
39 -20
16
4 5
-34 -8
-63 53
78 84
19 -16
64 9
-13 7
13 53
-20 4
2 -7
3 18
-12 10
-69 -93
2 9
27 64
-92 -100
Sample 2 Output
Yes
Yes
No
No
Yes
No
Yes
No
Yes
Yes
Yes
Yes
No
Yes
No
No