Problem7160--ABC252 —— G - Pre-Order

7160: ABC252 —— G - Pre-Order

[Creator : ]
Time Limit : 1.000 sec  Memory Limit : 256 MiB

SubmitSolved: 2Submit Num: 2StatisticsShowOff!

Description

There is a rooted tree with N vertices called Vertex $1, 2, \ldots…, N$, rooted at Vertex 1.
We performed a depth-first search starting at the root and obtained a preorder traversal of the tree: $P_1, P_2, \ldots, P_N$.
During the search, when the current vertex had multiple children, we chose the unvisited vertex with the smallest index.
What is a preorder traversal?
We start at the root and repeat the following procedure to list the vertices of the tree.
  • If the current vertex u is not recorded yet, record it.
  • Then, if u has an unvisited vertex, go to that vertex.
  • Otherwise, terminate if u is the root, and go to the parent of u if it is not.
    • The list of vertices in the order they are recorded here is the preorder traversal of the tree.
    Find the number of rooted trees consistent with the preorder traversal, modulo 998244353.
    Two rooted trees (with N vertices and rooted at Vertex 1) are considered different when there is a non-root vertex whose parent is different in the two trees.

    Input

    Input is given from Standard Input in the following format:
    $N$
    $P_1\ P_2\ \ldots\ P_N$

    Output

    Print the number of rooted trees consistent with the preorder traversal, modulo 998244353.

    Constraints

    $2≤N≤500$
    $1 \leq P_i\leq N$
    $P_1=1$
    All $P_i$ are distinct.
    All values in input are integers.

    Sample 1 Input 

    4
1 2 4 3

    Sample 1 Output 

    3

    The rooted trees consistent with the preorder traversal are the three shown below, so the answer is 3.

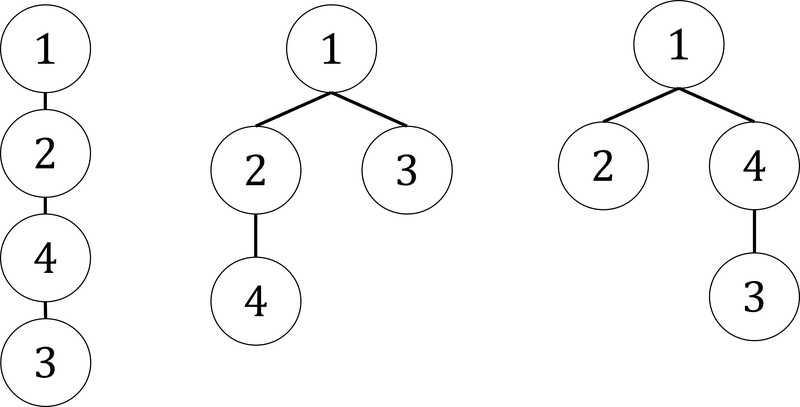
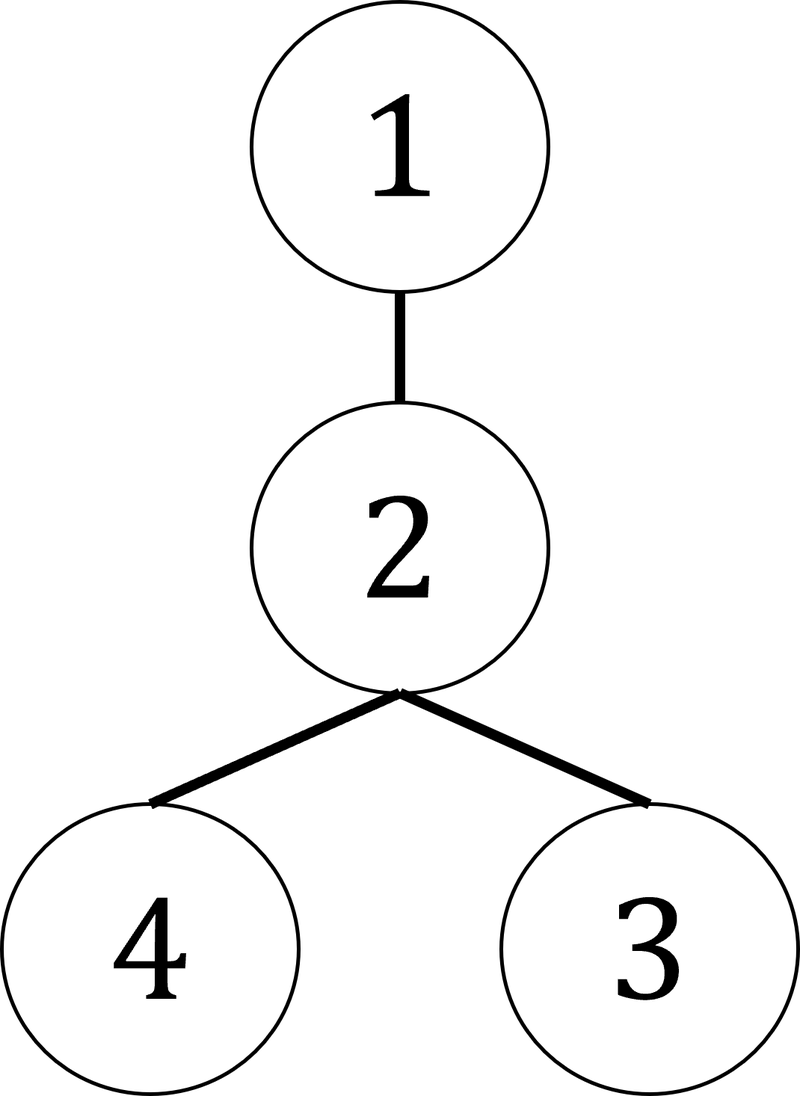
    Note that the tree below does not count. This is because, among the children of Vertex 2, we visit Vertex 3 before visiting Vertex 4, resulting in the preorder traversal 1,2,3,4.

    Sample 2 Input 

    8
1 2 3 5 6 7 8 4

    Sample 2 Output 

    202

    Source/Category

     
    Submit