7045: 「一本通 3.6 例 1」分离的路径
[Creator : ]
Description
原题来自:USACO 2006 Jan. Gold
为了从 F 个草场中的一个走到另一个,贝茜和她的同伴们不得不路过一些她们讨厌的可怕的树。奶牛们已经厌倦了被迫走某一条路,所以她们想建一些新路,使每一对草场之间都会至少有两条相互分离的路径,这样她们就有多一些选择。
每对草场之间已经有至少一条路径,给出所有 R 条双向路的描述,每条路连接了两个不同的草场,请计算最少的新建道路的数量。
路径由若干道路首尾相连而成,两条路径相互分离,是指两条路径没有一条重合的道路,但是两条分离的路径上可以有一些相同的草场。
对于同一对草场之间,可能已经有两条不同的道路,你也可以在它们之间再建一条道路,作为另一条不同的道路。
为了从 F 个草场中的一个走到另一个,贝茜和她的同伴们不得不路过一些她们讨厌的可怕的树。奶牛们已经厌倦了被迫走某一条路,所以她们想建一些新路,使每一对草场之间都会至少有两条相互分离的路径,这样她们就有多一些选择。
每对草场之间已经有至少一条路径,给出所有 R 条双向路的描述,每条路连接了两个不同的草场,请计算最少的新建道路的数量。
路径由若干道路首尾相连而成,两条路径相互分离,是指两条路径没有一条重合的道路,但是两条分离的路径上可以有一些相同的草场。
对于同一对草场之间,可能已经有两条不同的道路,你也可以在它们之间再建一条道路,作为另一条不同的道路。
Input
第一行输入两个整数 F 和 R;
接下来 R 行,每行输入两个整数,表示两个草场,它们之间有一条道路。
接下来 R 行,每行输入两个整数,表示两个草场,它们之间有一条道路。
Output
输出最少需要新建的道路数目。
Constraints
$1 \le F \le 5000,F-1 \le R \le 10000$。
Sample 1 Input
7 7
1 2
2 3
3 4
2 5
4 5
5 6
5 7
Sample 1 Output
2
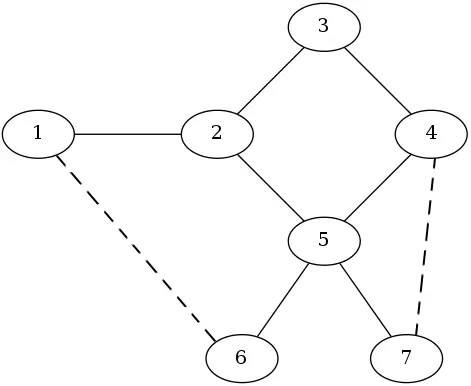
图中实线表示已有的道路,虚线表示新建的两条道路。现在可以检验一些路径,比如:
草场 1 和草场 2:$1 \to 2$ 和 $1\to 6 \to 5\to 2$
草场 1 和草场 4:$1\to 2 \to 3 \to 4$ 和 $1\to 6\to 5\to 4$
草场 3 和草场 7:$3\to 4\to 7$ 和 $3\to 2 \to 5\to 7$
事实上,每一对草场之间都连接了两条分离的路径。