6940: 学习系列 —— 传递闭包
[Creator : ]
Description
【定义】
传递闭包、即在数学中,在集合X上的二元关系 $R$ 的传递闭包是包含 $R$ 的 $X$ 上的最小的传递关系。
例如,如果 $X$ 是(生或死)人的集合而 $R$ 是关系“为父子”,则 $R$ 的传递闭包是关系“$x$ 是 $y$ 的祖先”。
再比如,如果 $X$ 是空港的集合而关系 $xRy$ 为“从空港 $x$ 到空港 $y$ 有直航”,则 $R$ 的传递闭包是“可能经一次或多次航行从 $x$ 飞到 $y$”。
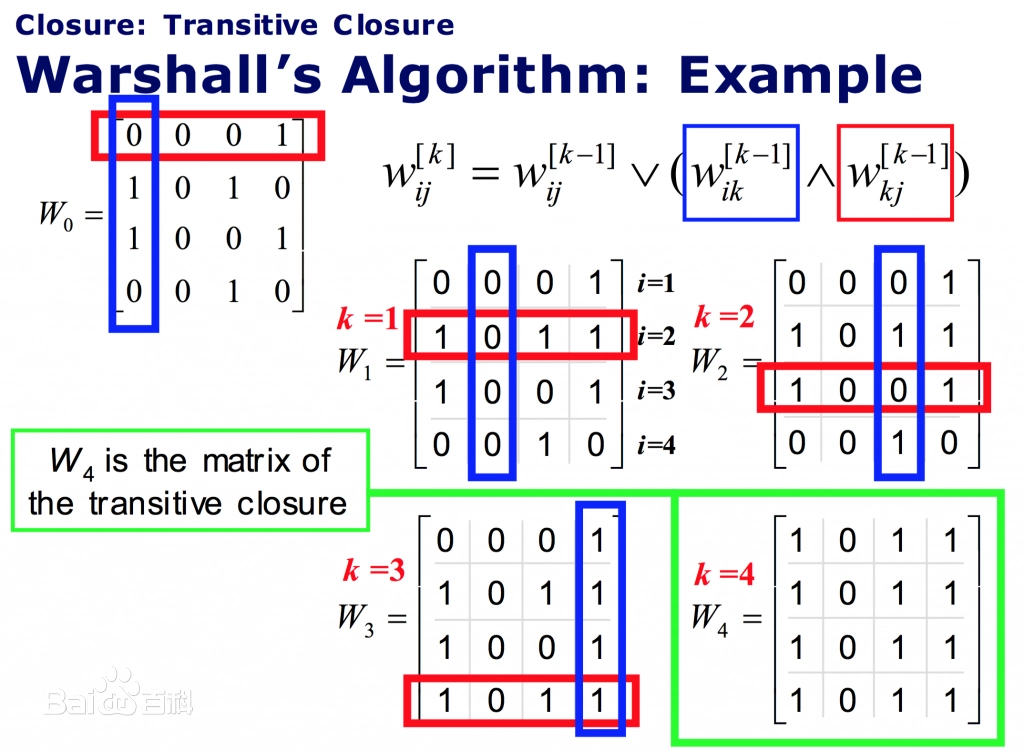
【算法】
传递闭包:通俗的讲就是如果 $a\to b,\ b \to c$,那么我们就建立一条 $a\to c$ 的边。将所有能间接相连的点直接相连。 Floyd 能在 $O(n^3)$ 求出一个图的传递闭包。
我们用 $d_{i,j}$ 表示原图,$g_{i,j}$ 表示它的传递闭包。
$g_{i,j}$ 是一个无权图,若从 $i$ 出发,可以到达 $j$ 则为 $1$,否则为 $0$。
时间复杂度 $O(V^3)$。
传递闭包、即在数学中,在集合X上的二元关系 $R$ 的传递闭包是包含 $R$ 的 $X$ 上的最小的传递关系。
例如,如果 $X$ 是(生或死)人的集合而 $R$ 是关系“为父子”,则 $R$ 的传递闭包是关系“$x$ 是 $y$ 的祖先”。
再比如,如果 $X$ 是空港的集合而关系 $xRy$ 为“从空港 $x$ 到空港 $y$ 有直航”,则 $R$ 的传递闭包是“可能经一次或多次航行从 $x$ 飞到 $y$”。

【算法】
传递闭包:通俗的讲就是如果 $a\to b,\ b \to c$,那么我们就建立一条 $a\to c$ 的边。将所有能间接相连的点直接相连。 Floyd 能在 $O(n^3)$ 求出一个图的传递闭包。
我们用 $d_{i,j}$ 表示原图,$g_{i,j}$ 表示它的传递闭包。
$g_{i,j}$ 是一个无权图,若从 $i$ 出发,可以到达 $j$ 则为 $1$,否则为 $0$。
时间复杂度 $O(V^3)$。
Input
【模板代码】
void warshall() {
for (int k=1; k<=n; k++) {//第一重循环为i→j的中间点k
for (int i=1; i<=n; i++) {//第二重循环为起点i
for (int j=1; j<=n; j++) {//第三重循环为终点j
//i-->k有边 且 k-->j有边 那么i-->j有边
if (g[i][k] && g[k][j]) {
g[i][j] = 1;
}
}
}
}
}