6884: 能量收集赛
[Creator : ]
Description
凯丽王国有 $n$ 座城市,每个城市都有一个能量值 $v_i$,$m$ 条单向道路连接着这些城市,但这些路不会构成环,即从任意一个城市出发,都无法回到这个城市。
而大马猴和机智羊要组队参加的下一个项目就是能量收集赛。能量收集赛的规则是:每位参赛者拿着一个能量值为 $0$ 的水晶球,从他所在的城市出发,每经过一个他从未到达的城市,就可以收集这个城市的能量值并加入自己的能量球中,直到走到无法再走为止。
所以每个参赛者都会收集尽可能多的能量。大马猴和机智羊都很聪明,他们在研究了地图之后,各自都能找到能量最多的路线。
然而当他们完成比赛之后,他们才被告知,他们是作为小组参赛,必须交上去两个能量值一样的能量球才行。他们研究发现,只要花费 $x\times(x+1)$ 的钱,就能将能量球的能量值从 $x$ 提升为 $x+1$。
鲨鱼博士想知道,如果大马猴一开始在城市 $q$,机智羊一开始在城市 $p$,那么:
而大马猴和机智羊要组队参加的下一个项目就是能量收集赛。能量收集赛的规则是:每位参赛者拿着一个能量值为 $0$ 的水晶球,从他所在的城市出发,每经过一个他从未到达的城市,就可以收集这个城市的能量值并加入自己的能量球中,直到走到无法再走为止。
所以每个参赛者都会收集尽可能多的能量。大马猴和机智羊都很聪明,他们在研究了地图之后,各自都能找到能量最多的路线。
然而当他们完成比赛之后,他们才被告知,他们是作为小组参赛,必须交上去两个能量值一样的能量球才行。他们研究发现,只要花费 $x\times(x+1)$ 的钱,就能将能量球的能量值从 $x$ 提升为 $x+1$。
鲨鱼博士想知道,如果大马猴一开始在城市 $q$,机智羊一开始在城市 $p$,那么:
-
大马猴和机智羊的成绩(刚完成比赛时)分别是多少?
-
为了使得他们的成绩有效,他们需要花费多少钱?
Input
第一行包含 $3$ 个正整数 $n,m,t$,分别表示城市的数量,单向道路的数量,询问次数。
第二行 $n$ 个正整数 $v_i$,依次表示每个城市的能量值。
接下来 $m$ 行,每行两个正整数 $x_i,\ y_i$,表示存在一条单向道路,可以从城市 $x_i$ 出发到达城市 $y_i$。
接下来 $t$ 行,每行两个正整数 $q,\ p$,表示大马猴和机智羊一开始所在的城市。
第二行 $n$ 个正整数 $v_i$,依次表示每个城市的能量值。
接下来 $m$ 行,每行两个正整数 $x_i,\ y_i$,表示存在一条单向道路,可以从城市 $x_i$ 出发到达城市 $y_i$。
接下来 $t$ 行,每行两个正整数 $q,\ p$,表示大马猴和机智羊一开始所在的城市。
Output
对于每次询问,输出一行,三个整数,以空格作为分割,分别表示大马猴和机智羊刚完成比赛时的成绩,以及想要使得成绩有效,需要花费的钱。
由于答案太大,请对 $10^9+7$ 取模。
由于答案太大,请对 $10^9+7$ 取模。
Constraints
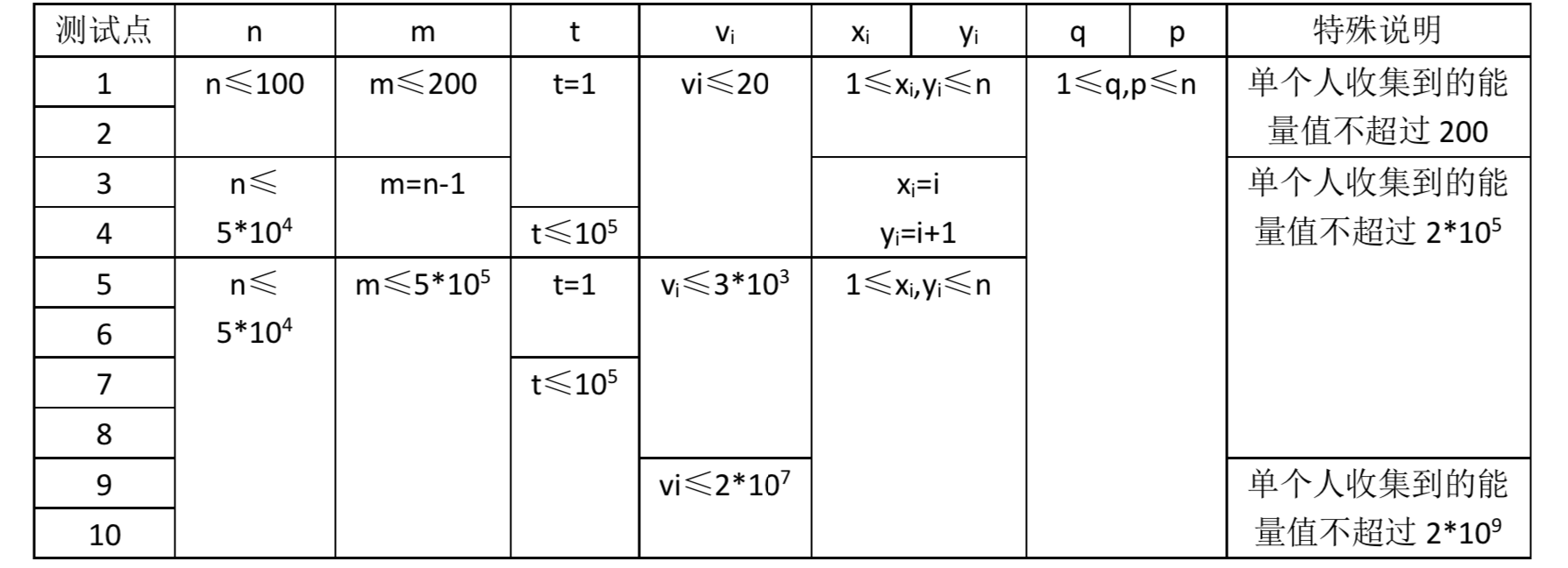
Sample 1 Input
5 6 1
1 1 1 1 1
1 2
1 3
2 5
3 4
3 5
4 5
1 2
Sample 1 Output
4 2 18
大马猴的路线为 $1\Rightarrow 3 \Rightarrow 4 \Rightarrow 5$,收集到的能量为 $1+1+1+1=4$;
机智羊的路线为 $2 \Rightarrow 5$,收集到的能量为 $1+1=2$;
想要让两个人的能量值一样,先将机智羊的能量从 $2$ 变为 $3$,即花费 $2\times 3$ 的钱;再从 $3$ 变为 $4$,即花费 $3\times 4$ 的钱,共 $2 \times 3+3 \times 4=18$。
机智羊的路线为 $2 \Rightarrow 5$,收集到的能量为 $1+1=2$;
想要让两个人的能量值一样,先将机智羊的能量从 $2$ 变为 $3$,即花费 $2\times 3$ 的钱;再从 $3$ 变为 $4$,即花费 $3\times 4$ 的钱,共 $2 \times 3+3 \times 4=18$。
Sample 2 Input
8 9 2
2 2 1 2 1 3 5 2
1 2
1 3
2 4
3 4
4 5
4 7
5 8
6 3
6 4
1 6
5 5
Sample 2 Output
11 11 0
3 3 0
对于第一次询问:
大马猴的路线为 $1\Rightarrow 2\Rightarrow 4\Rightarrow 7$,收集到的能量为 $2+2+2+5=11$;
机智羊的路线为 $6 \Rightarrow 3 \Rightarrow 4 \Rightarrow 7$,收集到的能量为 $3+1+2+5=11$;
两个人的能量值一样,成绩有效。
对于第二次询问:
两个人的路线都为 $5 \Rightarrow 8$,收集到的能量都为 $1+2=3$,显然成绩有效。
大马猴的路线为 $1\Rightarrow 2\Rightarrow 4\Rightarrow 7$,收集到的能量为 $2+2+2+5=11$;
机智羊的路线为 $6 \Rightarrow 3 \Rightarrow 4 \Rightarrow 7$,收集到的能量为 $3+1+2+5=11$;
两个人的能量值一样,成绩有效。
对于第二次询问:
两个人的路线都为 $5 \Rightarrow 8$,收集到的能量都为 $1+2=3$,显然成绩有效。