6881: 「一本通 1.4 练习 4」山峰和山谷
[Creator : ]
Description
FGD 小朋友特别喜欢爬山,在爬山的时候他就在研究山峰和山谷。
为了能够对旅程有一个安排,他想知道山峰和山谷的数量。
给定一个地图,为 FGD 想要旅行的区域,地图被分为 $n×n$ 的网格,每个格子 $(i,j)$ 的高度 $w(i,j)$ 是给定的。
若两个格子有公共顶点,那么它们就是相邻的格子,如与 $(i,j)$ 相邻的格子有 $(i−1,j−1),(i−1,j),(i−1,j+1),(i,j−1),(i,j+1),(i+1,j−1),(i+1,j),(i+1,j+1)$。
我们定义一个格子的集合 $S$ 为山峰(山谷)当且仅当:
为了能够对旅程有一个安排,他想知道山峰和山谷的数量。
给定一个地图,为 FGD 想要旅行的区域,地图被分为 $n×n$ 的网格,每个格子 $(i,j)$ 的高度 $w(i,j)$ 是给定的。
若两个格子有公共顶点,那么它们就是相邻的格子,如与 $(i,j)$ 相邻的格子有 $(i−1,j−1),(i−1,j),(i−1,j+1),(i,j−1),(i,j+1),(i+1,j−1),(i+1,j),(i+1,j+1)$。
我们定义一个格子的集合 $S$ 为山峰(山谷)当且仅当:
- $S$ 的所有格子都有相同的高度。
- $S$ 的所有格子都连通。
- 对于 $s$ 属于 $S$,与 $s$ 相邻的 $s^′$ 不属于 $S$,都有 $ws>w_{s^′}$(山峰),或者 $ws<w_{s^′}$(山谷)。
- 如果周围不存在相邻区域,则同时将其视为山峰和山谷。
Input
第一行包含一个正整数 $n$,表示地图的大小。
接下来一个 $n×n$ 的矩阵,表示地图上每个格子的高度 $w$。
接下来一个 $n×n$ 的矩阵,表示地图上每个格子的高度 $w$。
Output
共一行,包含两个整数,表示山峰和山谷的数量。
Constraints
$1≤n≤1000$,
$0≤w≤10^9$
$0≤w≤10^9$
Sample 1 Input
5
8 8 8 7 7
7 7 8 8 7
7 7 7 7 7
7 8 8 7 8
7 8 8 8 8
Sample 1 Output
2 1

Sample 2 Input
5
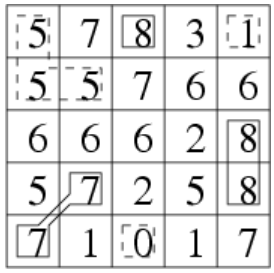
5 7 8 3 1
5 5 7 6 6
6 6 6 2 8
5 7 2 5 8
7 1 0 1 7
Sample 2 Output
3 3