定义

记忆化搜索是一种通过记录已经遍历过的状态的信息，从而避免对同一状态重复遍历的搜索实现方式。
因为记忆化搜索确保了每个状态只访问一次，它也是一种常见的动态规划实现方式。
记忆化搜索是一种典型的空间换时间的思想。记忆化搜索的典型应用场景是可能经过不同路径转移到相同状态的dfs问题。
记忆化搜索，本质还是动态规划，只是实现方式采用了 深度优先搜索 的形式，但是它不像 深度优先搜索那样 重复 枚举所有情况，而是把已经计算的子问题保存下来，这样就和动态规划的思想不谋而合了。

斐波那契数列

所谓斐波那契数列，是指一个数列【当前项】的值等于【前两项】之和：$f_i=f_{i-1}+f_{i-2}$。
对于 $f_5$ 的求解，程序调用如下：

使用递归的思路求解斐波那契数列的时间复杂度为 $O(\frac{2}{\sqrt{5}-1}^{n})$，这是一个指数级的算法。
递归求解斐波那契数列其实是一个深度优先搜索的过程，它是毫无优化的暴力枚举。
同时，我们也发现，计算过程中其实有很多重叠子问题，例如 
1. $f_3$ 被计算了 $2$ 次，如图所示。

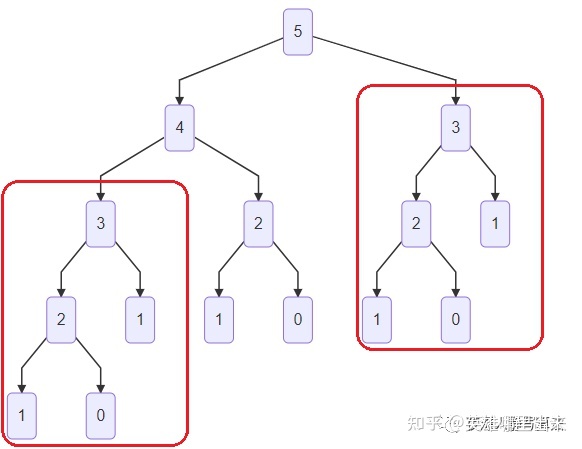
2. $f_2$ 被计算了 $3$ 次，如图所示

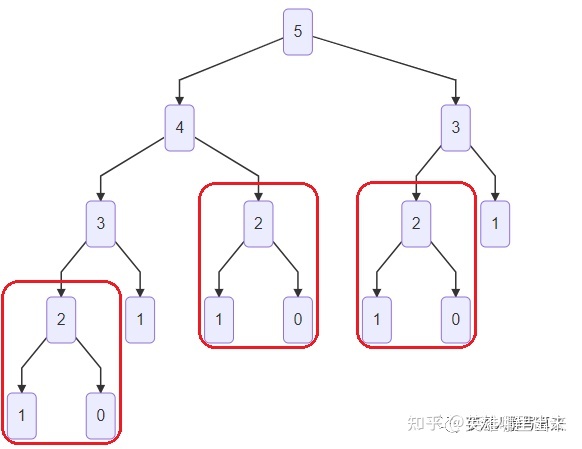
所以如果我们能够确保每个 $f_i$ 只被计算一次，问题就迎刃而解了。
可以考虑将 $f_i$ 计算出来的值存储到哈希数组 $h_i$ 中，当第二次要访问 $f_i$ 时，直接取 $h_i$ 的值即可，这样每次计算 $f_i$ 的时间复杂度变成了 $O(1)$ ，总共需要计算 $O(n)$。如下图所示。

这种用哈希数组来记录运算结果，避免重复运算的方法就是记忆化搜索。

记忆化搜索的含义

上面用一个简单的例子阐述了记忆化搜索的实现方式，并且提到了利用数组来记录已经计算出来的重叠子问题，这个和动态规划的思想非常相似，没错，记忆化搜索其实用的就是动态规划的思想。更加确切的说，可以用如下公式来表示：
                          记忆化搜索 = 深度优先搜索的实现 + 动态规划的思想
记忆化搜索深度优先搜索的实现动态规划的思想。