6815: 学习系列——排序—— 计数排序(Count sort)
[Creator : ]
Description
【算法概述】
计数排序是一个非基于比较的排序算法,元素从未排序状态变为已排序状态的过程,是由额外空间的辅助和元素本身的值决定的。
该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时,它的复杂度为 $Ο(n+k)$(其中 $k$ 是整数的范围),快于任何比较排序算法。当然这是一种牺牲空间换取时间的做法,而且当 $O(k)>O(nlogn)$ 的时候其效率反而不如基于比较的排序,因为基于比较的排序的时间复杂度在理论上的下限是 $O(nlogn)$。
【算法思路】
计数排序对输入的数据有附加的限制条件:
1、输入的线性表的元素属于有限偏序集 $S$;
2、设输入的线性表的长度为 $n$,$|S|=k$(表示集合 $S$ 中元素的总数目为 $k$),则 $k=O(n)$。
在这两个条件下,计数排序的复杂性为 $O(n)$。
计数排序的基本思想是对于给定的输入序列中的每一个元素 $x$,确定该序列中值小于 $x$ 的元素的个数(此处并非比较各元素的大小,而是通过对元素值的计数和计数值的累加来确定)。一旦有了这个信息,就可以将 $x$ 直接存放到最终的输出序列的正确位置上。
例如,如果输入序列中只有 $17$ 个元素的值小于 $x$ 的值,则 $x$ 可以直接存放在输出序列的第 $18$ 个位置上。
当然,如果有多个元素具有相同的值时,我们不能将这些元素放在输出序列的同一个位置上,因此,上述方案还要作适当的修改。
【算法过程】
先假设 20 个数列为:{9, 3, 5, 4, 9, 1, 2, 7, 8,1,3, 6, 5, 3, 4, 0, 10, 9, 7, 9}。
让我们先遍历这个无序的随机数组,找出最大值为 10 和最小值为 0。这样我们对应的计数范围将是 0 ~ 10。然后每一个整数按照其值对号入座,对应数组下标的元素进行加1操作。
比如第一个整数是 9,那么数组下标为 9 的元素加 1,如下图所示。

第二个整数是 3,那么数组下标为 3 的元素加 1,如下图所示。

继续遍历数列并修改数组......。最终,数列遍历完毕时,数组的状态如下图。

数组中的每一个值,代表了数列中对应整数的出现次数。
有了这个统计结果,排序就很简单了,直接遍历数组,输出数组元素的下标值,元素的值是几,就输出几次。比如统计结果中的 1 为 2,就是数列中有 2 个 1 的意思。这样我们就得到最终排序好的结果。
0, 1, 1, 2, 3, 3, 3, 4, 4, 5, 5, 6, 7, 7, 8, 9, 9, 9, 9, 10
【动画展示】
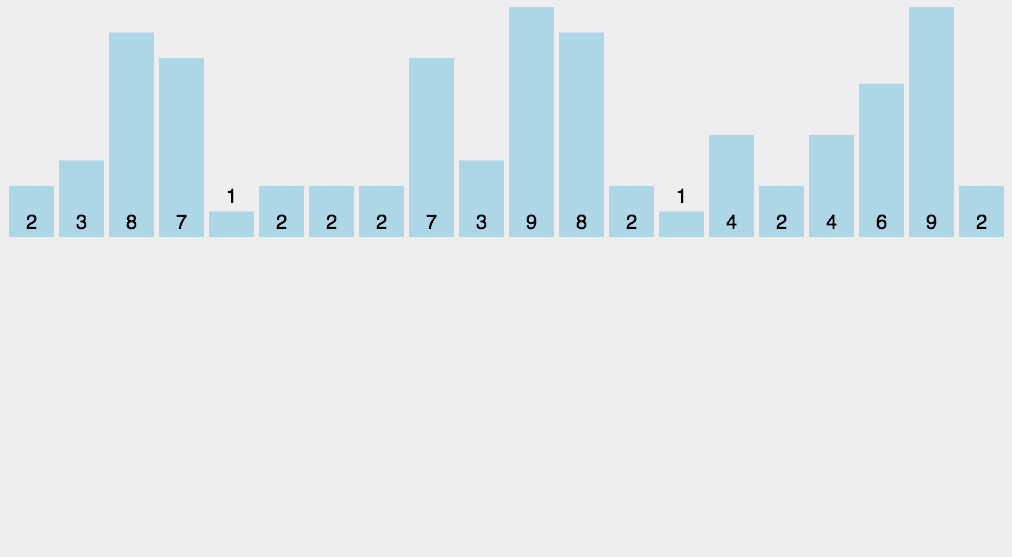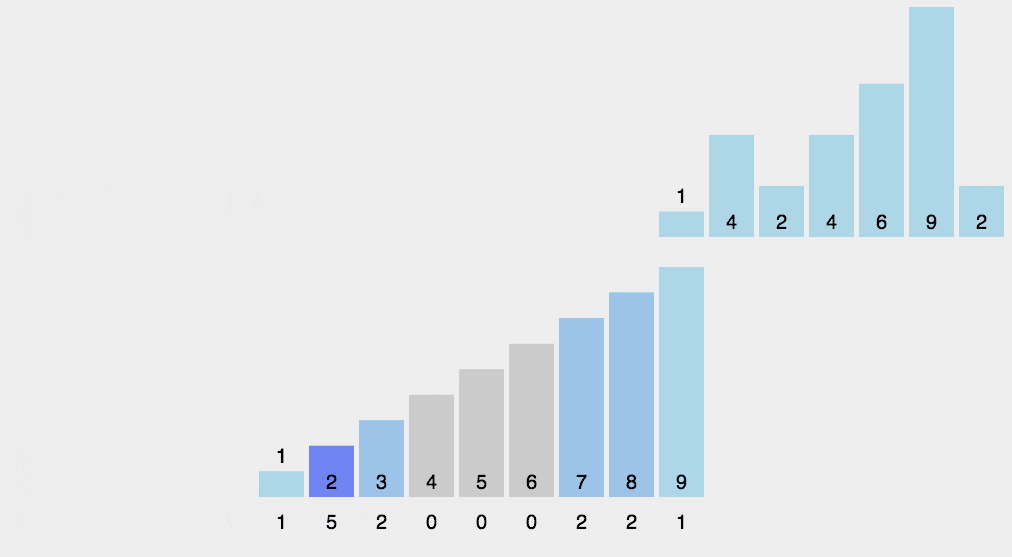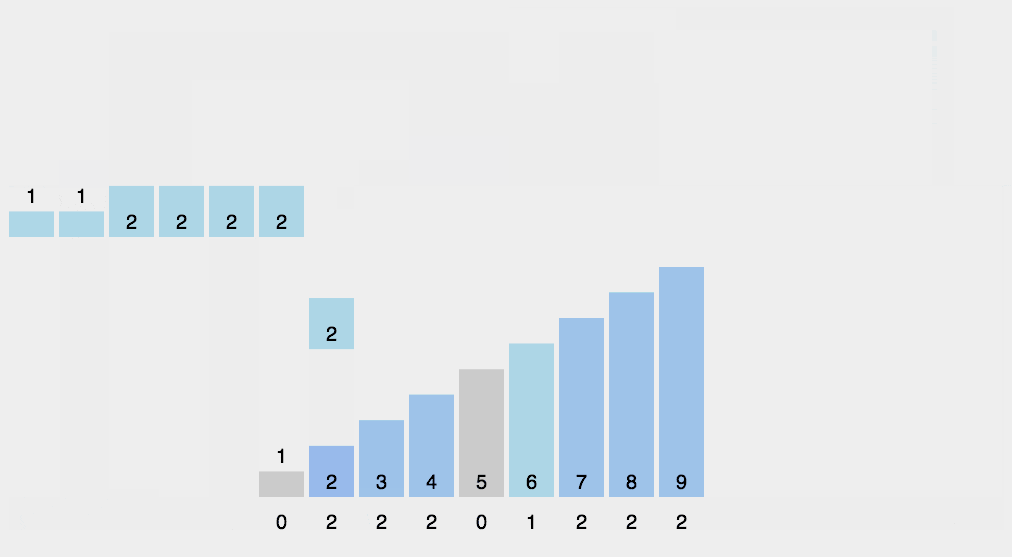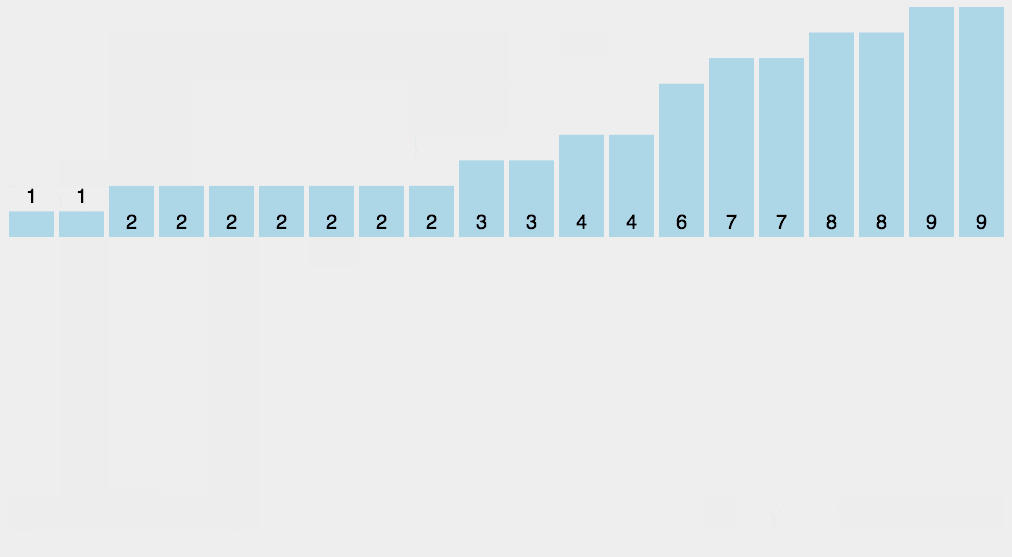
【时间复杂度】
$O(n+k)$。
【空间复杂度】
$O(k)$。
【稳定性】
稳定。
计数排序是一个非基于比较的排序算法,元素从未排序状态变为已排序状态的过程,是由额外空间的辅助和元素本身的值决定的。
该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时,它的复杂度为 $Ο(n+k)$(其中 $k$ 是整数的范围),快于任何比较排序算法。当然这是一种牺牲空间换取时间的做法,而且当 $O(k)>O(nlogn)$ 的时候其效率反而不如基于比较的排序,因为基于比较的排序的时间复杂度在理论上的下限是 $O(nlogn)$。
【算法思路】
计数排序对输入的数据有附加的限制条件:
1、输入的线性表的元素属于有限偏序集 $S$;
2、设输入的线性表的长度为 $n$,$|S|=k$(表示集合 $S$ 中元素的总数目为 $k$),则 $k=O(n)$。
在这两个条件下,计数排序的复杂性为 $O(n)$。
计数排序的基本思想是对于给定的输入序列中的每一个元素 $x$,确定该序列中值小于 $x$ 的元素的个数(此处并非比较各元素的大小,而是通过对元素值的计数和计数值的累加来确定)。一旦有了这个信息,就可以将 $x$ 直接存放到最终的输出序列的正确位置上。
例如,如果输入序列中只有 $17$ 个元素的值小于 $x$ 的值,则 $x$ 可以直接存放在输出序列的第 $18$ 个位置上。
当然,如果有多个元素具有相同的值时,我们不能将这些元素放在输出序列的同一个位置上,因此,上述方案还要作适当的修改。
【算法过程】
- 根据待排序集合中最大元素和最小元素的差值范围,申请额外空间;
- 遍历待排序集合,将每一个元素出现的次数记录到元素值对应的额外空间内;
- 对额外空间内数据进行计算,得出每一个元素的正确位置;
- 将待排序集合每一个元素移动到计算得出的正确位置上。
先假设 20 个数列为:{9, 3, 5, 4, 9, 1, 2, 7, 8,1,3, 6, 5, 3, 4, 0, 10, 9, 7, 9}。
让我们先遍历这个无序的随机数组,找出最大值为 10 和最小值为 0。这样我们对应的计数范围将是 0 ~ 10。然后每一个整数按照其值对号入座,对应数组下标的元素进行加1操作。
比如第一个整数是 9,那么数组下标为 9 的元素加 1,如下图所示。

第二个整数是 3,那么数组下标为 3 的元素加 1,如下图所示。

继续遍历数列并修改数组......。最终,数列遍历完毕时,数组的状态如下图。

数组中的每一个值,代表了数列中对应整数的出现次数。
有了这个统计结果,排序就很简单了,直接遍历数组,输出数组元素的下标值,元素的值是几,就输出几次。比如统计结果中的 1 为 2,就是数列中有 2 个 1 的意思。这样我们就得到最终排序好的结果。
0, 1, 1, 2, 3, 3, 3, 4, 4, 5, 5, 6, 7, 7, 8, 9, 9, 9, 9, 10
【动画展示】
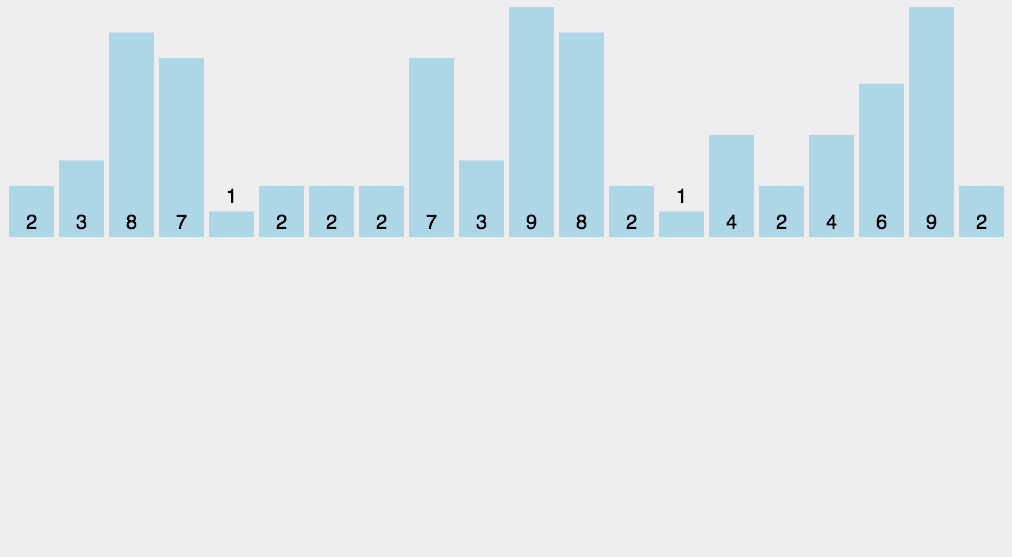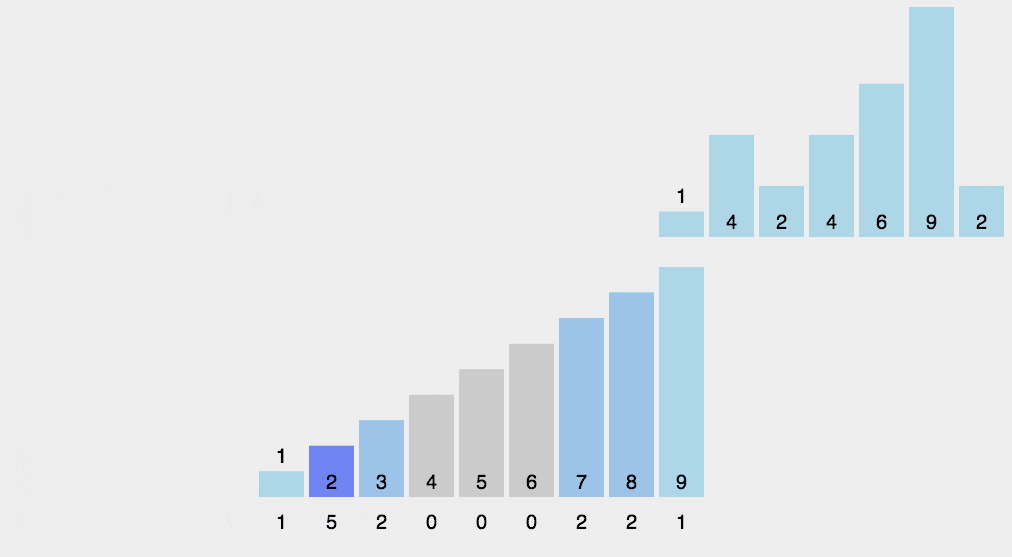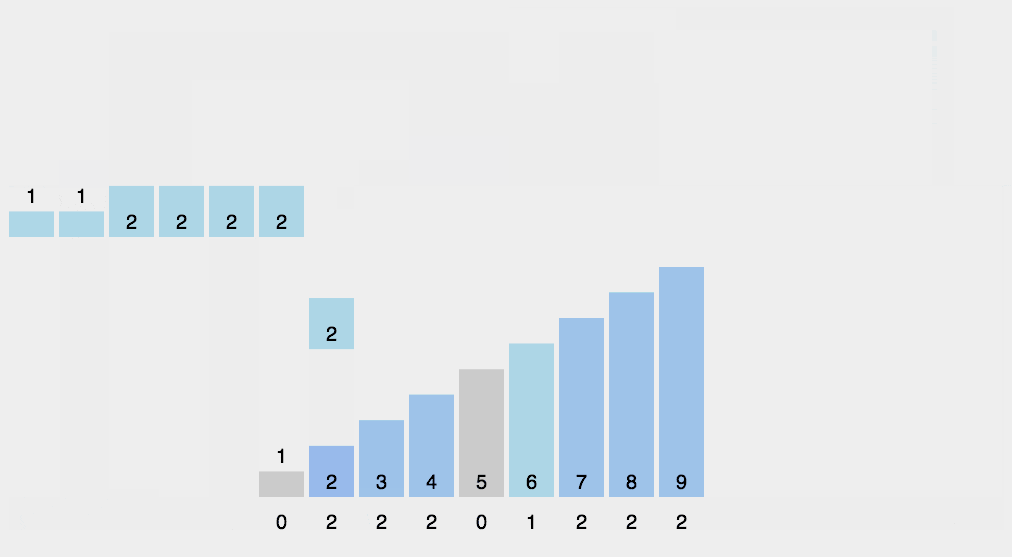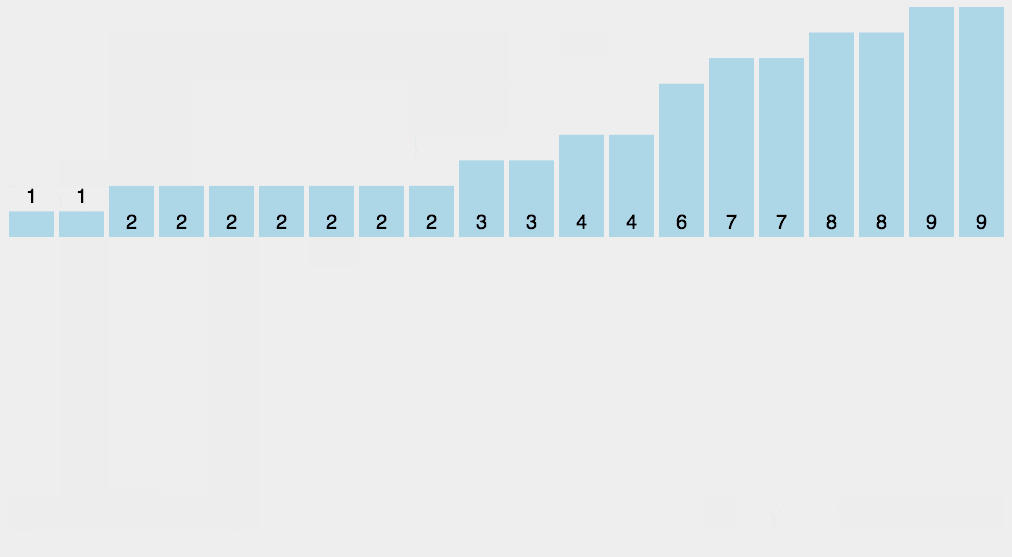
【时间复杂度】
$O(n+k)$。
【空间复杂度】
$O(k)$。
【稳定性】
稳定。