6778: 【学习系列】—— 字符串 —— 5. 最小循环节、循环周期
[Creator : ]
Description
引理:
对于某一字符串 $S[1 \sim i]$,在它众多的 next[i] 的“候选项”中,如果存在某一个 next[i],使得: i % (i−next[i])==0,那么 S[1 ~ (i−next[i])] 可以为 S[1 ~ i] 的循环元而 i/(i−next[i]) 即是它的循环次数 $K=i/(i-next[i])$。
证明:

如图,next[i]=j,由定义得红色部分两个子串完全相同。
那么有 S[1~j]=S[m~i] (m=i−next[i])。

如果我们在两个子串的前面框选一个长度为 m 的小子串(橙色部分)。
可以得到:S[1~m]=S[m~b]。
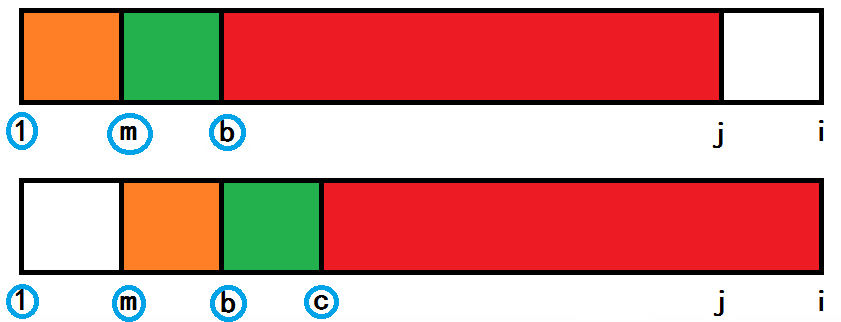
如果在紧挨着之前框选的子串后面再框选一个长度为 m 的小子串(绿色部分),同样的道理,
可以得到:S[m~b]=S[b~c]
又因为:S[1~m]=S[m~b]
所以:S[1~m]=S[m~b]=S[b~c]

如果一直这样框选下去,无限推进,总会有一个尽头。
当满足 i % m==0 时,刚好可以分出 $K$ 个这样的小子串,
且形成循环 (K=i/m)。
因此我们需要从 $1 \sim N$ 扫一遍,判断如果 next[i] 可以整除 $i$ ,即满足 i % (i−next[])==0,那么就可以肯定 S[1~ (i−next[i])] 是 S[1~i] 的最小循环元,而 i/(i−next[i]) 即是它的最大循环次数 $K$ ,直接依次输出这些 $i$ 和 $K$ 即可。
实际上由可以总结出很多结论:
结论一:
若 i−next[i] 可整除 $i$,则 s[1~i] 具有长度为 i−next[i] 的循环元,即 s[1~i−next[i]]。
结论二:
若 i−next[?] 可整除 $i$,则 s[1~i] 具有长度为 i−next[?] 的循环元,即 s[1~i−next[?]]。
结论三:
任意一个循环元的长度必定是最小循环元长度的倍数。
结论四:
如果 i−next[i] 不可整除 $i$,s[1~i−next[?]] 一定不能作为 s[1~i] 的循环元。
【模板题】
6775
6777
6779
对于某一字符串 $S[1 \sim i]$,在它众多的 next[i] 的“候选项”中,如果存在某一个 next[i],使得: i % (i−next[i])==0,那么 S[1 ~ (i−next[i])] 可以为 S[1 ~ i] 的循环元而 i/(i−next[i]) 即是它的循环次数 $K=i/(i-next[i])$。
证明:

如图,next[i]=j,由定义得红色部分两个子串完全相同。
那么有 S[1~j]=S[m~i] (m=i−next[i])。

如果我们在两个子串的前面框选一个长度为 m 的小子串(橙色部分)。
可以得到:S[1~m]=S[m~b]。

如果在紧挨着之前框选的子串后面再框选一个长度为 m 的小子串(绿色部分),同样的道理,
可以得到:S[m~b]=S[b~c]
又因为:S[1~m]=S[m~b]
所以:S[1~m]=S[m~b]=S[b~c]

如果一直这样框选下去,无限推进,总会有一个尽头。
当满足 i % m==0 时,刚好可以分出 $K$ 个这样的小子串,
且形成循环 (K=i/m)。
因此我们需要从 $1 \sim N$ 扫一遍,判断如果 next[i] 可以整除 $i$ ,即满足 i % (i−next[])==0,那么就可以肯定 S[1~ (i−next[i])] 是 S[1~i] 的最小循环元,而 i/(i−next[i]) 即是它的最大循环次数 $K$ ,直接依次输出这些 $i$ 和 $K$ 即可。
实际上由可以总结出很多结论:
结论一:
若 i−next[i] 可整除 $i$,则 s[1~i] 具有长度为 i−next[i] 的循环元,即 s[1~i−next[i]]。
结论二:
若 i−next[?] 可整除 $i$,则 s[1~i] 具有长度为 i−next[?] 的循环元,即 s[1~i−next[?]]。
结论三:
任意一个循环元的长度必定是最小循环元长度的倍数。
结论四:
如果 i−next[i] 不可整除 $i$,s[1~i−next[?]] 一定不能作为 s[1~i] 的循环元。
【模板题】
6775
6777
6779