6764: 【学习系列】—— 字符串 —— 4. KMP算法
[Creator : ]
Description
KMP 算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris 和 V.R.Pratt 同时发现,因此人们称它为克努特——莫里斯——普拉特操作(简称 KMP 算法)。
KMP 算法的关键是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是实现一个 next() 函数,函数本身包含了模式串的局部匹配信息。时间复杂度 $O(m+n)$。

上方为朴素算法即按位比较,下方为 KMP 算法实现的字符串比较方式。KMP 可以通过较少的比较次数完成匹配。
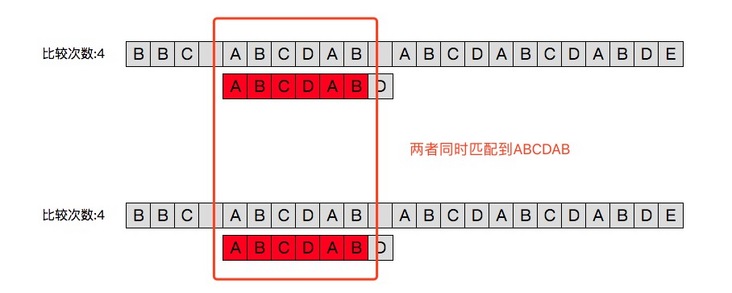
与朴素算法一致,在之前对于主串 “BBC ” 的匹配中模式串 ABCBABD 的第一个字符均与之不同故向后移位到现在上图所示的位置。主串通过依次与模式串中的字符比较我们可以看出,模式串的前 $6$ 个字符与主串相同即 ABCDAB;而这也就是 KMP 算法的关键。

朴素算法雷打不动得向后移了一位。而 KMP 跳过了主串的 BCD 三个字符。从而进行了一次避免无意义的移位比较。那么它是怎么知道我这次要跳过三个而不是两个或者不跳呢?关键在于上一次已经匹配的部分 ABCDAB。
第一次匹配失败时的情形如下:
为了从已匹配部分提取信息。现在将主串做一下变形:
我们现在只知道已匹配的部分,因为匹配已经失败了不会再去读取后面的字符,故用 X 代替。
那么我们能跳过多少位置的问题就可以由下面的解得知答案:
答案自然是如下移动:
因为我们不知道 X 代表什么,只能从已匹配的串来分析。故我们能跳过部分位置的依据是什么?
答:已匹配的模式串的前 $n$ 位能否等于匹配部分的主串的后 $n$ 位。并且 $n$ 尽可能大。
举个例子:
现在 KMP 的基本思路已经很明显了,其就是通过经失败后得知的已匹配字段,来寻找主串尾部与模式串头部的相同最大匹配,如果有则可以跨过中间的部分,因为所谓“中间”的部分,也是有可能进入主串尾与模式串头的,没进去的原因即是相对位置字符不同,故最终在模式串移位时可以跳过。
之前叙述的在已匹配部分中查找主串头部与模式串尾部相同的部分的结果我们可以用部分匹配值的说法来形容:
答:匹配串长度 - 部分匹配值;本次例子中为 $6-2=4$,模式串向右移动四位。
$$\pi[i] = \max_{k = 0 \dots i}\{k: s[0 \dots k - 1] = s[i - (k - 1) \dots i]\}$$
特别地,规定 $\pi[0]=0$。
举例来说,对于字符串 abcabcd,
$\pi[0]=0$,因为 a 没有真前缀和真后缀,根据规定为 0
$\pi[1]=0$,因为 ab 真前缀为 {a},真后缀为 {b},无相等的真前缀和真后缀
$\pi[2]=0$,因为 abc 真前缀为 {a,ab},真后缀为 {bc,c},无相等的真前缀和真后缀
$\pi[3]=1$,因为 abca 真前缀为 {a,ab,abc},真后缀为 {bca,bc,a},只有一对相等的真前缀和真后缀:a,长度为 1
$\pi[4]=2$,因为 abcab 真前缀为 {a,ab,abc,abca},真后缀为 {bcab,cab,ab,a},相等的真前缀和真后缀只有 ab,长度为 2
$\pi[5]=3$,因为 abcabc 真前缀为 {a,ab,abc,abca,abcab},真后缀为 {bcabc,cabc,abc,ab,a}, 相等的真前缀和真后缀只有 abc,长度为 3
$\pi[6]=0$,因为 abcabcd 真前缀为 {a,ab,abc,abca,abcabc},真后缀为 {bcabcd,cabcd,abcd,abcd,bc,d},无相等的真前缀和真后缀
同理可以计算字符串 aabaaab 的前缀函数为 $[0,1,0,1,2,2,3]$。
首先,字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符,进行比较。因为B与A不匹配,所以搜索词后移一位。

因为B与A不匹配,搜索词再往后移。

就这样,直到字符串有一个字符,与搜索词的第一个字符相同为止。

接着比较字符串和搜索词的下一个字符,还是相同。

直到字符串有一个字符,与搜索词对应的字符不相同为止。

这时,最自然的反应是,将搜索词整个后移一位,再从头逐个比较。这样做虽然可行,但是效率很差,因为你要把"搜索位置"移到已经比较过的位置,重比一遍。

一个基本事实是,当空格与D不匹配时,你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是,设法利用这个已知信息,不要把"搜索位置"移回已经比较过的位置,继续把它向后移,这样就提高了效率。
怎么做到这一点呢?可以针对搜索词,算出一张《部分匹配表》(Partial Match Table)

已知空格与D不匹配时,前面六个字符"ABCDAB"是匹配的。查表可知,最后一个匹配字符B对应的"部分匹配值"为2,因此按照下面的公式算出向后移动的位数:
移动位数 = 已匹配的字符数 - 对应的部分匹配值
因为 $6 - 2$ 等于 $4$,所以将搜索词向后移动 $4$ 位。

因为空格与C不匹配,搜索词还要继续往后移。这时,已匹配的字符数为2("AB"),对应的"部分匹配值"为0。所以,移动位数 = 2 - 0,结果为 2,于是将搜索词向后移2位。

因为空格与A不匹配,继续后移一位。

逐位比较,直到发现C与D不匹配。于是,移动位数 = 6 - 2,继续将搜索词向后移动4位。

逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动7位,这里就不再重复了。

那么,最长相同前缀和后缀你也应该能找出来了吧

最长相同前后缀不能是字符串本身,因为如果你认为最长相同前后缀可以是字符串本身的话,那么这就是一个恒成立的命题了。

"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例,
- "A"的前缀和后缀都为空集,共有元素的长度为0;
- "AB"的前缀为[A],后缀为,共有元素的长度为0;
- "ABC"的前缀为[A, AB],后缀为[BC, C],共有元素的长度0;
- "ABCD"的前缀为[A, AB, ABC],后缀为[BCD, CD, D],共有元素的长度为0;
- "ABCDA"的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素为"A",长度为1;
- "ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],共有元素为"AB",长度为2;
- "ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为[BCDABD, CDABD, DABD, ABD, BD, D],共有元素的长度为0。
上述代码中总共有三个地方如果能理解清楚这个代码也就没问题了。
next[0]=-1,next[j]=l,k=next[k],其中k=next[k]最让人摸不着头脑
A:next[0]=-1
首先是next[0]=-1,如下当目标串的第一个位置,也就是索引为0的位置,发生不匹配时,应该让目标串的索引为-1的位置与当前不匹配的地方对齐比较

好的,我知道你肯定回文,怎么可能有-1的位置啊,这明显越界了啊?你先不要管这些,我就问你,这种情况下,是不是应该是目标串的第一个位置与主串的下一个位置进行比较? 是的,的确是这样,所以我这里先截取,KMP算法的一小段(不要担心你肯定看得懂)

上面的j=next[j]不用不说在干什么了,好的回到上面的问题,此时就是执行结果就是-1=next[0],也就是j=-1了,然后重新回到循环,继续判断,此时j=-1,进入if内,注意i++,j++,请问i++是在干什么?,而j++会等于0,这不就是让目标串的第一位与主串的下一位比较吗
所以你现在能理解为什么next[0]=-1了吧
B:next[j]=k
首先next[j]=k我认为大家肯定能明白的一点就是在为next数组进行位置,但是不明白的是为什么下标为j的元素的值是k
那么我想问哪种情况下会有next[j]=k?,根据上面的代码自然是k=-1或str[j]=str[k]的时候。
好的现在,我们先考虑k=-1,当k=-1时,总会有k++,使得k变为0,这样的话next[j]=0,表明前面没有相同的前后缀
那么一旦k不是-1,满足这个if的唯一条件就是str[j]=str[k]了。如果此刻str[j]=str[k],这就表示此时的位置可以算作相同的前后缀了,我们所做的就是判断下一对了。
比如下面,可以看出,此时k来到了C的位置,j也来到了C的位置,他们之前都各自在B的位置,由于相同,所以来到了现在位置,现在他们要判断此刻对应的位置是否可以也将其算入相同的前后缀。

非常幸运,他们相同,于是j++,k++,next[j]=3

如下,j和k准备比较下一个

很遗憾这个位置,无法使其成为长度为4的相同前后缀,那么根据代码只能执行k=next[k]了
这样画比较难受,我把前缀直接拿到下面来

有没有似曾相识的感觉?没错,好像是主串和目标串,但是这不是原来的那个两个串。而是后缀作为了主串,前缀作为了目标串,好的,现在前缀(目标串)的下表为3的位置发生了不匹配,该怎么做?这不用问我吧,当然是让前缀(目标串)下标为1的位置(next[3]=1)与该不匹配处重新比较
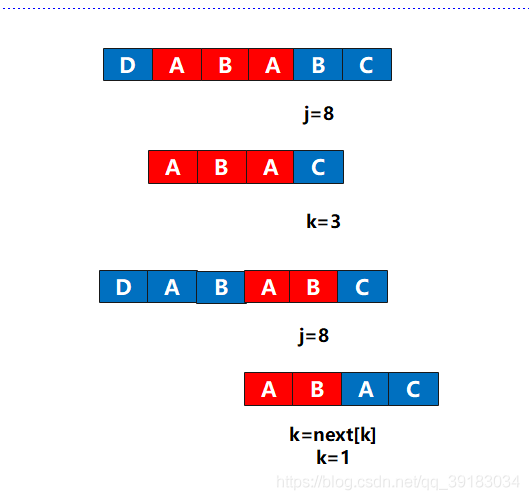
好的,重新组装回去,毕竟这不是真的主串和目标串
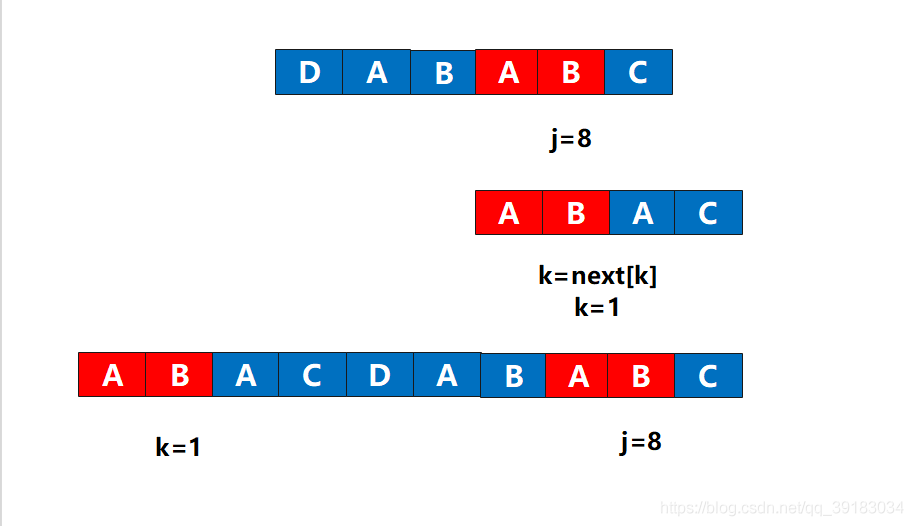
好的,现在if的判断是否满足,当然满足,对应位置相同,那么继续i++,j++,于是next[9]=2,此时next数组全部赋值完成。
这就是为什么这样回溯的原因!
仔细想一想,下面的这种情况中已经不可能有ABAB,ABAC相等的情况存在了,因为一旦相同,那么next[9]=4了,也即是C之前不可能有长度为4的相同的前后缀,但是没有这么长的或许也有短的呀,你看咋们上面的那个AB=AB不就是一个短的情况吗,所以这也就是为什么有k=next[k]这样的回溯的情况。其实就是在前缀和后缀在比较,只不过一旦遇到不相等,前人栽树后人乘凉罢了!
如果你能理解最后的那句谚语,那么这个算法你应该掌握的八九不离十了,这里也可以看出这个算法有多么的牛逼,简直即使巧妙之际,不得不佩服发明KMP算法的这三位大牛的聪明才智啊

KMP 算法的关键是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是实现一个 next() 函数,函数本身包含了模式串的局部匹配信息。时间复杂度 $O(m+n)$。
BBC ABCDAB ABCDABCDABDE 为主串; ABCDABD 为模式串

上方为朴素算法即按位比较,下方为 KMP 算法实现的字符串比较方式。KMP 可以通过较少的比较次数完成匹配。
基本思路
从上图的效果预览中可以看出使用朴素算法依次比较模式串需要移位 $13$ 次,而使用 KMP 需要 $8$ 次,故可以说 KMP 的思路是通过避免无效的移位,来快速移动到指定的地点。接下来我们关注一下 KMP 是如何“跳着”移动的:
与朴素算法一致,在之前对于主串 “BBC ” 的匹配中模式串 ABCBABD 的第一个字符均与之不同故向后移位到现在上图所示的位置。主串通过依次与模式串中的字符比较我们可以看出,模式串的前 $6$ 个字符与主串相同即 ABCDAB;而这也就是 KMP 算法的关键。
根据已知信息计算下一次移位位置
我们先从下图来看朴素算法与 KMP 中下一次移位的过程:
朴素算法雷打不动得向后移了一位。而 KMP 跳过了主串的 BCD 三个字符。从而进行了一次避免无意义的移位比较。那么它是怎么知道我这次要跳过三个而不是两个或者不跳呢?关键在于上一次已经匹配的部分 ABCDAB。
从已匹配部分发掘信息
我们已知此时主串与模式串均有此相同的部分 ABCDAB。那么如何从这共同部分中获得有用的信息?或者换个角度想一下:我们能跳过部分位置的依据是什么?第一次匹配失败时的情形如下:
BBC ABCDAB ABCDABCDABDE
ABCDABD
D != 空格 故失败
为了从已匹配部分提取信息。现在将主串做一下变形:
ABCDABXXXXXX... X可能是任何字符
我们现在只知道已匹配的部分,因为匹配已经失败了不会再去读取后面的字符,故用 X 代替。
那么我们能跳过多少位置的问题就可以由下面的解得知答案:
//ABCDAB向后移动几位可能能匹配上?
ABCDABXXXXXX...
ABCDABD
答案自然是如下移动:
ABCDABXXXXXX...
ABCDABD
因为我们不知道 X 代表什么,只能从已匹配的串来分析。故我们能跳过部分位置的依据是什么?
答:已匹配的模式串的前 $n$ 位能否等于匹配部分的主串的后 $n$ 位。并且 $n$ 尽可能大。
举个例子:
//第一次匹配失败时匹配到ABCDDDABC为共同部分
XXXABCDDDABCFXXX
ABCDDDABCE
//寻找模式串的最大前几位与主串匹配到的部分后几位相同,
//可以发现最多是ABC部分相同,故可以略过DDD的匹配因为肯定对不上
XXXABCDDDABCFXXX
ABCDDDABCE
现在 KMP 的基本思路已经很明显了,其就是通过经失败后得知的已匹配字段,来寻找主串尾部与模式串头部的相同最大匹配,如果有则可以跨过中间的部分,因为所谓“中间”的部分,也是有可能进入主串尾与模式串头的,没进去的原因即是相对位置字符不同,故最终在模式串移位时可以跳过。
部分匹配值
上面是用通俗的话来述说我们如何根据已匹配的部分来决定下一次模式串移位的位置,大家应该已经大体知道 KMP 的思路了。现在来引出官方的说法。之前叙述的在已匹配部分中查找主串头部与模式串尾部相同的部分的结果我们可以用部分匹配值的说法来形容:
- 其中定义"前缀"和"后缀"。"前缀"指除了最后一个字符以外,一个字符串的全部头部组合;"后缀"指除了第一个字符以外,一个字符串的全部尾部组合。
- "部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。
- 前缀分别为 A、AB、ABC、ABCD、ABCDA
- 后缀分别为 B、AB、DAB、CDAB、BCDAB
答:匹配串长度 - 部分匹配值;本次例子中为 $6-2=4$,模式串向右移动四位。
前缀函数定义
给定一个长度为 $n$ 的字符串 $s$,其 前缀函数 被定义为一个长度为 $n$ 的数组 $\pi$。 其中 $\pi[i]$ 的定义是:- 如果子串 $s[0...i]$ 有一对相等的真前缀与真后缀:$s[0...k-1]$ 和 $s[i-(k-1)...i]$,那么 $\pi[i]$ 就是这个相等的真前缀(或者真后缀,因为它们相等:))的长度,也就是 $\pi[i]=k$;
- 如果不止有一对相等的,那么 $\pi[i]$ 就是其中最长的那一对的长度;
- 如果没有相等的,那么 $\pi[i]=0$。
$$\pi[i] = \max_{k = 0 \dots i}\{k: s[0 \dots k - 1] = s[i - (k - 1) \dots i]\}$$
特别地,规定 $\pi[0]=0$。
举例来说,对于字符串 abcabcd,
$\pi[0]=0$,因为 a 没有真前缀和真后缀,根据规定为 0
$\pi[1]=0$,因为 ab 真前缀为 {a},真后缀为 {b},无相等的真前缀和真后缀
$\pi[2]=0$,因为 abc 真前缀为 {a,ab},真后缀为 {bc,c},无相等的真前缀和真后缀
$\pi[3]=1$,因为 abca 真前缀为 {a,ab,abc},真后缀为 {bca,bc,a},只有一对相等的真前缀和真后缀:a,长度为 1
$\pi[4]=2$,因为 abcab 真前缀为 {a,ab,abc,abca},真后缀为 {bcab,cab,ab,a},相等的真前缀和真后缀只有 ab,长度为 2
$\pi[5]=3$,因为 abcabc 真前缀为 {a,ab,abc,abca,abcab},真后缀为 {bcabc,cabc,abc,ab,a}, 相等的真前缀和真后缀只有 abc,长度为 3
$\pi[6]=0$,因为 abcabcd 真前缀为 {a,ab,abc,abca,abcabc},真后缀为 {bcabcd,cabcd,abcd,abcd,bc,d},无相等的真前缀和真后缀
同理可以计算字符串 aabaaab 的前缀函数为 $[0,1,0,1,2,2,3]$。
KMP 算法实现
下面先直接给出 KMP 的算法流程(如果感到一点点不适,没关系,坚持下,稍后会有具体步骤及解释,越往后看越会柳暗花明☺):
-
假设现在文本串 $S$ 匹配到 $i$ 位置,模式串 $P$ 匹配到 $j$ 位置
- 如果 j = -1,或者当前字符匹配成功(即 S[i] == P[j]),都令i++,j++,继续匹配下一个字符;
-
如果 j != -1,且当前字符匹配失败(即 S[i] != P[j]),则令 i 不变,j = next[j]。此举意味着失配时,模式串 $P$ 相对于文本串 $S$ 向右移动了 j - next [j] 位。
- 换言之,当匹配失败时,模式串向右移动的位数为:失配字符所在位置 - 失配字符对应的 next 值(next 数组的求解会在下文的中详细阐述),即移动的实际位数为:j - next[j],且此值大于等于 1。
此也意味着在某个字符失配时,该字符对应的 next 值会告诉你下一步匹配中,模式串应该跳到哪个位置(跳到 next[j] 的位置)。如果 next[j] 等于 0 或 -1,则跳到模式串的开头字符,若 next[j] = k 且 k > 0,代表下次匹配跳到 j 之前的某个字符,而不是跳到开头,且具体跳过了 k 个字符。
首先,字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符,进行比较。因为B与A不匹配,所以搜索词后移一位。

因为B与A不匹配,搜索词再往后移。

就这样,直到字符串有一个字符,与搜索词的第一个字符相同为止。

接着比较字符串和搜索词的下一个字符,还是相同。

直到字符串有一个字符,与搜索词对应的字符不相同为止。

这时,最自然的反应是,将搜索词整个后移一位,再从头逐个比较。这样做虽然可行,但是效率很差,因为你要把"搜索位置"移到已经比较过的位置,重比一遍。

一个基本事实是,当空格与D不匹配时,你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是,设法利用这个已知信息,不要把"搜索位置"移回已经比较过的位置,继续把它向后移,这样就提高了效率。
怎么做到这一点呢?可以针对搜索词,算出一张《部分匹配表》(Partial Match Table)

已知空格与D不匹配时,前面六个字符"ABCDAB"是匹配的。查表可知,最后一个匹配字符B对应的"部分匹配值"为2,因此按照下面的公式算出向后移动的位数:
移动位数 = 已匹配的字符数 - 对应的部分匹配值
因为 $6 - 2$ 等于 $4$,所以将搜索词向后移动 $4$ 位。

因为空格与C不匹配,搜索词还要继续往后移。这时,已匹配的字符数为2("AB"),对应的"部分匹配值"为0。所以,移动位数 = 2 - 0,结果为 2,于是将搜索词向后移2位。

因为空格与A不匹配,继续后移一位。

逐位比较,直到发现C与D不匹配。于是,移动位数 = 6 - 2,继续将搜索词向后移动4位。

逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动7位,这里就不再重复了。
最长相同前缀和后缀

那么,最长相同前缀和后缀你也应该能找出来了吧

最长相同前后缀不能是字符串本身,因为如果你认为最长相同前后缀可以是字符串本身的话,那么这就是一个恒成立的命题了。

"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例,
- "A"的前缀和后缀都为空集,共有元素的长度为0;
- "AB"的前缀为[A],后缀为,共有元素的长度为0;
- "ABC"的前缀为[A, AB],后缀为[BC, C],共有元素的长度0;
- "ABCD"的前缀为[A, AB, ABC],后缀为[BCD, CD, D],共有元素的长度为0;
- "ABCDA"的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素为"A",长度为1;
- "ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],共有元素为"AB",长度为2;
- "ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为[BCDABD, CDABD, DABD, ABD, BD, D],共有元素的长度为0。
KMP 算法实现
void next(const string &p) {
LL j=0,k=-1;
next[0]=-1;
while(j<p.size()) {
if(k == -1 || p[j] == p[k]) {
j++;k++;
next[j] = k;
}
else k = next[k];//此语句是这段代码最反人类的地方,如果你一下子就能看懂,那么请允许我称呼你一声大神!
}
}
你说它长也就算了,毕竟是一个具有难度的算法,但是它偏偏这么短,这就让人很尴尬。 上述代码中总共有三个地方如果能理解清楚这个代码也就没问题了。
next[0]=-1,next[j]=l,k=next[k],其中k=next[k]最让人摸不着头脑
A:next[0]=-1
首先是next[0]=-1,如下当目标串的第一个位置,也就是索引为0的位置,发生不匹配时,应该让目标串的索引为-1的位置与当前不匹配的地方对齐比较

好的,我知道你肯定回文,怎么可能有-1的位置啊,这明显越界了啊?你先不要管这些,我就问你,这种情况下,是不是应该是目标串的第一个位置与主串的下一个位置进行比较? 是的,的确是这样,所以我这里先截取,KMP算法的一小段(不要担心你肯定看得懂)

上面的j=next[j]不用不说在干什么了,好的回到上面的问题,此时就是执行结果就是-1=next[0],也就是j=-1了,然后重新回到循环,继续判断,此时j=-1,进入if内,注意i++,j++,请问i++是在干什么?,而j++会等于0,这不就是让目标串的第一位与主串的下一位比较吗
所以你现在能理解为什么next[0]=-1了吧
B:next[j]=k
首先next[j]=k我认为大家肯定能明白的一点就是在为next数组进行位置,但是不明白的是为什么下标为j的元素的值是k
那么我想问哪种情况下会有next[j]=k?,根据上面的代码自然是k=-1或str[j]=str[k]的时候。
好的现在,我们先考虑k=-1,当k=-1时,总会有k++,使得k变为0,这样的话next[j]=0,表明前面没有相同的前后缀
那么一旦k不是-1,满足这个if的唯一条件就是str[j]=str[k]了。如果此刻str[j]=str[k],这就表示此时的位置可以算作相同的前后缀了,我们所做的就是判断下一对了。
比如下面,可以看出,此时k来到了C的位置,j也来到了C的位置,他们之前都各自在B的位置,由于相同,所以来到了现在位置,现在他们要判断此刻对应的位置是否可以也将其算入相同的前后缀。

非常幸运,他们相同,于是j++,k++,next[j]=3

C:k=next[k]
我认为kmp算法的高潮部分就在这里!(为了方便说明,我换了一张图)如下,j和k准备比较下一个

很遗憾这个位置,无法使其成为长度为4的相同前后缀,那么根据代码只能执行k=next[k]了
这样画比较难受,我把前缀直接拿到下面来

有没有似曾相识的感觉?没错,好像是主串和目标串,但是这不是原来的那个两个串。而是后缀作为了主串,前缀作为了目标串,好的,现在前缀(目标串)的下表为3的位置发生了不匹配,该怎么做?这不用问我吧,当然是让前缀(目标串)下标为1的位置(next[3]=1)与该不匹配处重新比较

好的,重新组装回去,毕竟这不是真的主串和目标串

好的,现在if的判断是否满足,当然满足,对应位置相同,那么继续i++,j++,于是next[9]=2,此时next数组全部赋值完成。
这就是为什么这样回溯的原因!
仔细想一想,下面的这种情况中已经不可能有ABAB,ABAC相等的情况存在了,因为一旦相同,那么next[9]=4了,也即是C之前不可能有长度为4的相同的前后缀,但是没有这么长的或许也有短的呀,你看咋们上面的那个AB=AB不就是一个短的情况吗,所以这也就是为什么有k=next[k]这样的回溯的情况。其实就是在前缀和后缀在比较,只不过一旦遇到不相等,前人栽树后人乘凉罢了!
如果你能理解最后的那句谚语,那么这个算法你应该掌握的八九不离十了,这里也可以看出这个算法有多么的牛逼,简直即使巧妙之际,不得不佩服发明KMP算法的这三位大牛的聪明才智啊

Input
理解 next 数组的含义:$next[i]$ 表示前面长度为 $i$ 的子串中,前缀和后缀相等的最大长度。
如:abcdabc
如对于a,ab,abc,abcd,很明显,前缀和后缀相同的长度为 $0$
对于长度为 $5$ 的子串 abcda,前缀的 a 和后缀的 a 相同,长度为 $1$
对于长度为 $6$ 的子串 abcdab,前缀的 ab 和后缀的 ab 相同,长度为 $2$
对于长度为 $7$ 的子串 abcdabc,前缀的 abc 和后缀的 abc 相同,长度为 $3$
如:abcdabc
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 字符 | a | b | c | d | a | b | c |
|
| next | -1 | 0 | 0 | 0 | 0 | 1 | 2 | 3 |
如对于a,ab,abc,abcd,很明显,前缀和后缀相同的长度为 $0$
对于长度为 $5$ 的子串 abcda,前缀的 a 和后缀的 a 相同,长度为 $1$
对于长度为 $6$ 的子串 abcdab,前缀的 ab 和后缀的 ab 相同,长度为 $2$
对于长度为 $7$ 的子串 abcdabc,前缀的 abc 和后缀的 abc 相同,长度为 $3$
Output
【模板代码】
/*
* KMP
* nxt[i]表示字串 s[1...i] 最长的相等的真前缀与真后缀的长度。
* 时间复杂度:O(n+m),其中n是搜索串长度,m是模式串长度
*/
std::vector<int> nxt;
//求next数组
void kmp_next(const std::string &p){
//注意,我们使用字符串从下标1开始
int m=p.size()-1;
//重置数组数据
nxt.assign(m+1,0);
for(int i=2,j=0; i<=m; i++){
while(j && p[i]!=p[j+1]){
//找到最长的前后缀重叠长度
j=nxt[j];
}
if(p[i]==p[j+1]){
j++;
}
nxt[i]=j;
}
}
//匹配操作
int kmp(const std::string &s, const std::string &p){
int cnt=0;
kmp_next(p);
//注意,我们使用字符串从下标1开始
int n=s.size()-1;
int m=p.size()-1;
for(int i=1,j=0; i<=n; i++){
while(j && s[i]!=p[j+1]){
//不匹配,利用next往回跳
j=nxt[j];
}
if(s[i]==p[j+1]){
//匹配,则匹配下一位
j++;
}
if(j==m){
//满足匹配条件
//根据题目处理,比如输出答案之类
//cout<<i-m<<" ";
cnt++;
j=nxt[j];//再次匹配
}
}
return cnt;
}