6617: ABC202 —— E - Count Descendants
[Creator : ]
Description
We have a rooted tree with NN vertices, numbered $1, 2, \dots, N$.
Vertex $1$ is the root, and the parent of Vertex $i\ (2 \leq i \leq N)$ is Vertex $P_i$.
You are given $Q$ queries. In the $i$-th query $(1 \leq i \leq Q)$, given integers $U_i$ and $D_i$, find the number of vertices $u$ that satisfy all of the following conditions:
Vertex $1$ is the root, and the parent of Vertex $i\ (2 \leq i \leq N)$ is Vertex $P_i$.
You are given $Q$ queries. In the $i$-th query $(1 \leq i \leq Q)$, given integers $U_i$ and $D_i$, find the number of vertices $u$ that satisfy all of the following conditions:
- Vertex $U_i$ is in the shortest path from $u$ to the root (including the endpoints).
- There are exactly $D_i$ edges in the shortest path from $u$ to the root.
Input
Input is given from Standard Input in the following format:
$N$
$P_2\ P_3\ \ldots\ P_N$
$Q$
$U_1\ D_1$
$U_2\ D_2$
$\vdots$
$U_Q\ D_Q$
$N$
$P_2\ P_3\ \ldots\ P_N$
$Q$
$U_1\ D_1$
$U_2\ D_2$
$\vdots$
$U_Q\ D_Q$
Output
Print $Q$ lines. The $i$-th line should contain the response to the $i$-th query.
Constraints
$2≤N≤2×10^5$
$1 \leq P_i < i$
$1 \leq Q \leq 2 \times 10^5$
$1 \leq U_i \leq N$
$0 \leq D_i \leq N - 1$
All values in input are integers.
$1 \leq P_i < i$
$1 \leq Q \leq 2 \times 10^5$
$1 \leq U_i \leq N$
$0 \leq D_i \leq N - 1$
All values in input are integers.
Sample 1 Input
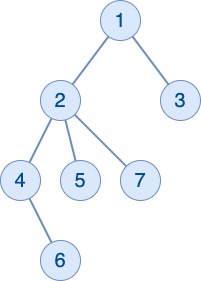
7
1 1 2 2 4 2
4
1 2
7 2
4 1
5 5
Sample 1 Output
3
1
0
0
In the $1$-st query, Vertices $4, 5$, and $7$ satisfy the conditions. In the $2$-nd query, only Vertices $7$ satisfies the conditions. In the $3$-rd and $4$-th queries, no vertice satisfies the conditions.