6586: 学习系列 —— 最大公约数
[Creator : ]
Description
【知识点】
欧几里得算法(又称辗转相除法)用于计算两个数的最大公约数,被称为世界上最古老的算法。现在人们已无法确定该算法具体的提出时间,但其最早被发现记载于公元前 300 年欧几里得的著作中,因此得以命名。
【过程】
假设我们需要求 $1112$ 和 $695$ 的最大公约数。
首先用较小的数字去除较大的数字,求出余数。也就是对两个数字进行 mod 运算。$1112\ \bmod\ 695=417$。

接下来再用除数 $695$ 和余数 $417$ 进行 $\bmod$ 运算。结果为 $278$。

继续重复同样的操作,对 $417$和 $278$ 进行 $\bmod$ 运算,结果为 $139$。

对 $278$ 和 $139$ 进行 $\bmod$ 运算,结果为 $0$。也就是说,$278$ 可以被 $139$ 整除。
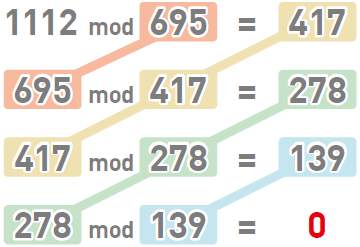
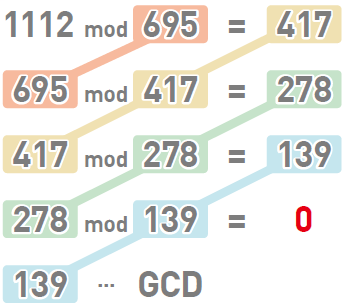
余数为 $0$ 时,最后一次运算中的除数 $139$ 就是 $1112$ 和 $695$ 的最大公约数。
【最大公约数性质】
1、结合律。 $gcd(a,b,c)=gcd(a, gcd(b, c)) = gcd(gcd(a, b), c)$。
2、$gcd(a,b)=gcd(b, \frac{a}{b})=gcd(b, \lvert a-b \rvert)=gcd(a, \lvert a-b \rvert)$。
欧几里得算法(又称辗转相除法)用于计算两个数的最大公约数,被称为世界上最古老的算法。现在人们已无法确定该算法具体的提出时间,但其最早被发现记载于公元前 300 年欧几里得的著作中,因此得以命名。
【过程】
假设我们需要求 $1112$ 和 $695$ 的最大公约数。
首先用较小的数字去除较大的数字,求出余数。也就是对两个数字进行 mod 运算。$1112\ \bmod\ 695=417$。

接下来再用除数 $695$ 和余数 $417$ 进行 $\bmod$ 运算。结果为 $278$。

继续重复同样的操作,对 $417$和 $278$ 进行 $\bmod$ 运算,结果为 $139$。

对 $278$ 和 $139$ 进行 $\bmod$ 运算,结果为 $0$。也就是说,$278$ 可以被 $139$ 整除。

余数为 $0$ 时,最后一次运算中的除数 $139$ 就是 $1112$ 和 $695$ 的最大公约数。

【最大公约数性质】
1、结合律。 $gcd(a,b,c)=gcd(a, gcd(b, c)) = gcd(gcd(a, b), c)$。
2、$gcd(a,b)=gcd(b, \frac{a}{b})=gcd(b, \lvert a-b \rvert)=gcd(a, \lvert a-b \rvert)$。