6574: 学习系列 —— 计算几何 —— 向量的概念极其表示方式
[Creator : ]
Description
【向量】
向量 (英语:euclidean vector,物理、工程等也称作矢量 、欧几里得向量)是数学、物理学和工程科学等多个自然科学中的基本概念。指一个同时具有大小和方向,且满足平行四边形法则的几何对象。在二维空间中引入一组正交基矢量 $\{i,j\}$,一般成右手系,则该平面的任一向量均可唯一确定地表示为这组基矢量的线性组合: $v=v_xi+v_yj$。
【如何表示一个向量】
数学上的向量通常可用加向右箭头的小写字母表示。
如上图所示,给定两点 $\displaystyle A, \displaystyle B$ 时,也可确定一固定向量:如确定一个始于点从 $\displaystyle A$ 终于点 $\displaystyle B$ 的向量,符号表示为:$\overrightarrow{AB}$。
【向量运算】
【加法】
向量的加法满足平行四边形法则和三角形法则。具体地,两个向量 $\vec {a}$ 和 $\vec {b}$ 相加,得到的是另一个向量。这个向量可以表示为 $\vec {a}$ 和 $\vec {b}$ 的起点重合后,以它们为邻边构成的平行四边形的一条对角线(以共同的起点为起点的那一条,见下图左),或者表示为将 $\vec {a}$ 的终点和 $\vec{b}$ 的起点重合后,从$\vec{a}$ 的起点指向 $\vec{b}$ 的终点的向量: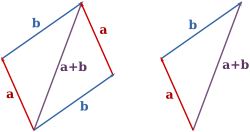
【减法】
两个向量 $\vec{a}$ 和 $\vec{b}$ 的相减,则可以看成是向量 $\vec{a}$ 加上一个与 $\vec{b}$ 大小相等,方向相反的向量。又或者,$\vec{a}$ 和 $\vec{b}$ 的相减得到的向量可以表示为 $\vec{a}$ 和 $\vec{b}$ 的起点重合后,从 $\vec{b}$ 的终点指向 $\vec{a}$ 的终点的向量: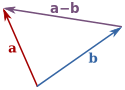
【点乘】
两个向量的点乘得到一个标量。我们假设 $\vec{a}$ 和 $\vec{b}$ 是 $n$ 维向量。$\vec{a} \cdot \vec{b}=a_1 \cdot b_1 + a_2 \cdot b_2 + \cdots + a_n \cdot b_n$
点乘的几何含义:
点乘的几何意义是可以用来表征或计算两个向量之间的夹角,以及在 $\vec{b}$ 向量在 $\vec{a}$ 向量方向上的投影,有公式:
$\vec{a} \cdot \vec{b}=|a||b|\cos \theta$
点乘反映着两个向量的“相似度”,两个向量越“相似”,它们的点乘越大。
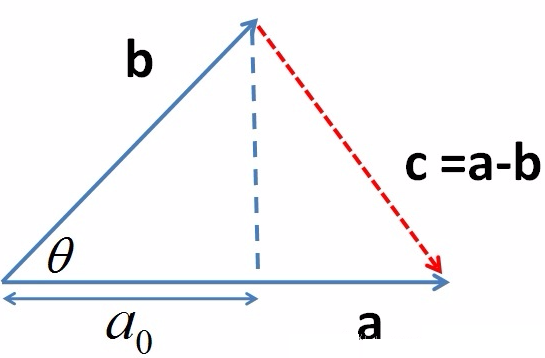
进一步作用:判断两个向量是否同一方向或正交(即垂直)等方向关系。
$\vec{a} \cdot \vec{b} > 0$,说明两个向量夹角 $\theta$ 在 $[0^\circ, 90^\circ)$,也就是两个向量方向相同。
$\vec{a} \cdot \vec{b} = 0$,说明两个向量夹角 $\theta=90^\circ$。也就是两个向量正交,互相垂直。
$\vec{a} \cdot \vec{b} < 0$,说明两个向量夹角 $\theta$ 在 $(90^\circ, 180^\circ]$,也就是两个向量方向相反。
【叉乘】
它也是向量与向量的乘积,不过需要注意的是,它的结果是个向量。它的几何意义是所得的向量与被乘向量所在平面垂直,方向由右手定则规定,大小是两个被乘向量张成的平行四边形的面积。所以向量积不满足交换律。为了简化,我们假设$\vec{a}$ 和 $\vec{b}$ 是 $2$ 维向量,则其向量积的矩阵表达式可用下列符号表示:
$\vec{a} \times \vec{b}=\begin{vmatrix} \vec{i} & \vec{j} \\ a_x & a_y \\ b_x & b_y \end{vmatrix}=(a_xb_y)\vec{i}-(b_xa_y)\vec{j}$
在 3D 图像学中,外积的概念非常有用,可以通过两个向量的外积,生成第三个垂直于a,b的法向量,从而构建X、Y、Z坐标系。如下图所示:
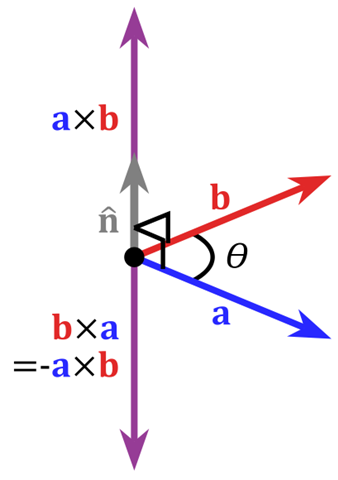
在二维空间中,外积还有另外一个几何意义就是:$|a×b|$ 在数值上等于由向量a和向量b构成的平行四边形的面积。
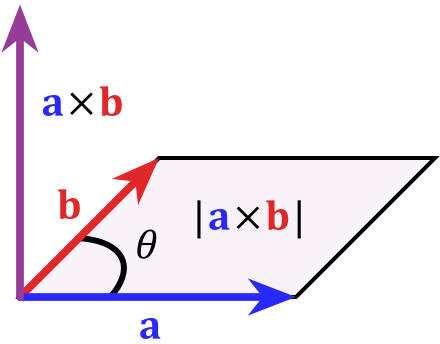
叉乘的几何含义:
$\vec{a} \times \vec{b}=|a|*|b|*\sin \theta$
$\overrightarrow{P_0P_1}$ 和 $\overrightarrow{P_0P_2}$,对它们的公共端点 $P_0$ 来说,判断 $P_0P_1$ 是否在 $P_0P_2$ 的顺时针方向。
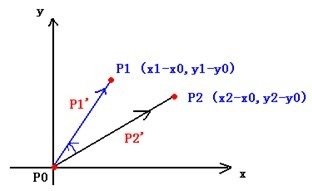
如上图,吧 $P_0$ 作为原点,得到向量 $P_1^{\prime}=P_1-P_0$ 和 $P_2^{\prime}=P_2-P_0$,计算 $P_1^{\prime} \times P_2^{\prime}$ 的叉乘即可。
- 如果叉乘为正数,说明 $P_1^\prime, P_2^\prime$ 是顺时针方向。
- 如果叉乘为负数,说明 $P_1^\prime, P_2^\prime$ 是逆时针方向。
- 如果叉乘为零,说明 $P_0, P_1, P_2$ 是三点共线。
Input
【向量】
在OI中,我们直接用点表示向量。const double EPS=1e-10;
struct POINT{
double x,y;//点坐标
//构造函数
POINT(double x=0,double y=0):x(x),y(y){
}
//重载符号运算
//向量加
POINT operator+(const POINT &p) const {
return POINT(x+p.x,y+p.y);
}
//向量减
POINT operator-(const POINT &p) const{
return POINT(x-p.x,y-p.y);
}
//乘标量
POINT operator*(double a) const {
return POINT(x*a,y*a);
}
//除标量
POINT operator/(double a) const{
return POINT(x/a,y/a);
}
//比较
bool operator<(const POINT &p) const{
return x!=p.x?x<p.x:y<p.y;
}
//判断相等
bool operator==(const POINT &p) const{
return fabs(x-p.x)<EPS&&fabs(y-p.y)<EPS;
}
//计算norm
double norm() const{
return x*x+y*y;
}
//向量模长
double length() const{
return sqrt(norm());
}
};
//定义向量
typedef POINT VECTOR;
【点乘(dot product)】
设向量 $\vec{a}, \vec{b}$ 的夹角为 $\theta\ (0 \leq \theta \leq 180)$,那么 $\vec{a}, \vec{b}$ 的内积 $a \cdot b=|a||b|\text{cos}\theta$。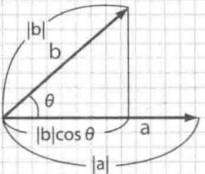
根据余弦定理 $\text{cos}\theta=\frac{|a|^2+|b|^2-|b-a|^2}{2|a||b|}$ 可知,$a \cdot b=\frac{|a|^2+|b|^2-|b-a|^2}{2}=a_x \times b_x+a_y \times b_y$。
也就是说 $a \cdot b=|a||b|\text{cos}\theta=a_x \times b_x+a_y \times b_y$。
//点乘
double dot(const VECTOR &a, const VECTOR &b){
return a.x*b.x+a.y*b.y;
}
【叉乘(cross product)】
设向量 $\vec{a}, \vec{b}$ 的夹角为 $\theta\ (0 \leq \theta \leq 180)$,那么 $\vec{a}, \vec{b}$ 的外积 $a \times b=|a||b|\text{sin}\theta$。也就是 $|a \times b|=|a||b|\text{sin}\theta =a_x \times b_y-a_y \times b_x$。
//叉乘
double cross(const VECTOR &a, const VECTOR &b){
return a.x*b.y-a.y*b.x;
}
叉积的结果也是一个向量,是垂直于 $\vec{a},\ \vec{b}$ 所形成的平面。