6572: 数山峰(二)
[Creator : ]
Description
在平面直角坐标系上有 $n$ 座像山峰一样的图案。每座山峰是一个直角等腰三角形,它们的底边都是坐标系的 $X$ 轴,它们的峰顶在第一象限里,其中第 $i$ 座山峰的峰顶坐标为 $(x_i,y_i)$。
如果一座山峰的一部分在另一座山峰的内部,那么这两部分山峰就重叠了。给定每个山峰的峰顶坐标,请统计不重复计算重叠部分的前提下,这些山峰的总面积是多少。
如果一座山峰的一部分在另一座山峰的内部,那么这两部分山峰就重叠了。给定每个山峰的峰顶坐标,请统计不重复计算重叠部分的前提下,这些山峰的总面积是多少。
Input
第一行:单个整数 $n$;
第二行到第 $n+1$ 行:第 $i+1$ 行两个整数,表示一个峰顶的坐标 $x_i,y_i$。
第二行到第 $n+1$ 行:第 $i+1$ 行两个整数,表示一个峰顶的坐标 $x_i,y_i$。
Output
单个整数:设所有的山峰的可见面积为 $s$,因为希望输出整数,所以规定输出 $4 \times s$。
Constraints
对于 $30\%$ 的数据,$1\leq n\leq 1,000$;
对于 $60\%$ 的数据,$1\leq n\leq 10,000$;
对于 $100\%$ 的数据,$1\leq n\leq 100,000$;
$1\leq x_i, y_i\leq 100,000,000$。
对于 $60\%$ 的数据,$1\leq n\leq 10,000$;
对于 $100\%$ 的数据,$1\leq n\leq 100,000$;
$1\leq x_i, y_i\leq 100,000,000$。
Sample 1 Input
3
1 1
2 1
4 1
Sample 1 Output
11
前两个山峰有交集,面积为 $1+1+1-0.25=2.75$。
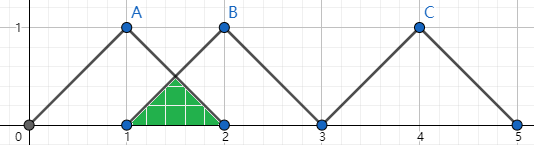

Sample 2 Input
4
1 1
3 1
5 2
8 1
Sample 2 Output
27
Sample 3 Input
3
5 5
2 1
4 1
Sample 3 Output
100