【知识点】
平衡二叉查找树：简称平衡二叉树。由前苏联的数学家 Adelse-Velskil 和 Landis 在 1962 年提出的高度平衡的二叉树，根据科学家的英文名也称为 AVL 树。
它是一种特殊的二叉排序树，具有以下性质的二叉树：
（1）可以是空树；
（2）左子树和右子树都是平衡二叉树；
（3）左子树和右子树的深度（高度）之差的绝对值不超过1。
该结构下对树中节点的查询、删除和插入三种操作，时间复杂度均为 $O(log_2N) \sim O(N)$。影响时间复杂度的因素即为二叉树的高，为了尽量避免树中每层上只有一个节点的情况。

【平衡因子】
定义：某节点的左子树与右子树的高度(深度)差即为该节点的平衡因子（BF,Balance Factor），平衡二叉树中不存在平衡因子大于 1 的节点。在一棵平衡二叉树中，节点的平衡因子只能取 0、1 或者 -1 ，分别对应着左右子树等高，左子树比较高，右子树比较高。
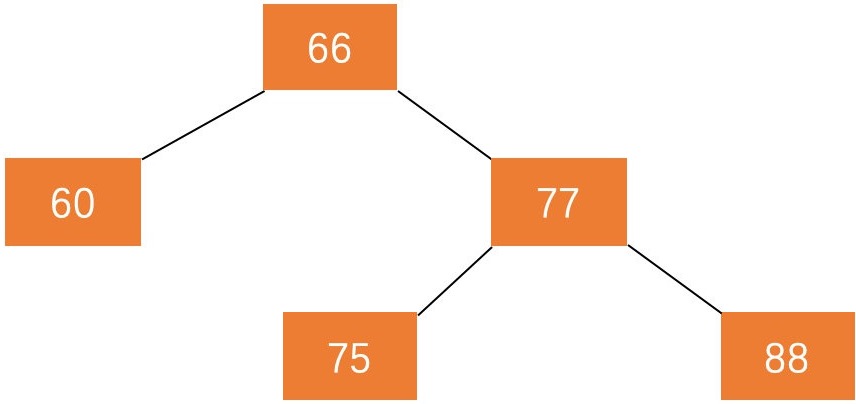
例如下图为平衡因子为 $0$ 的 AVL。



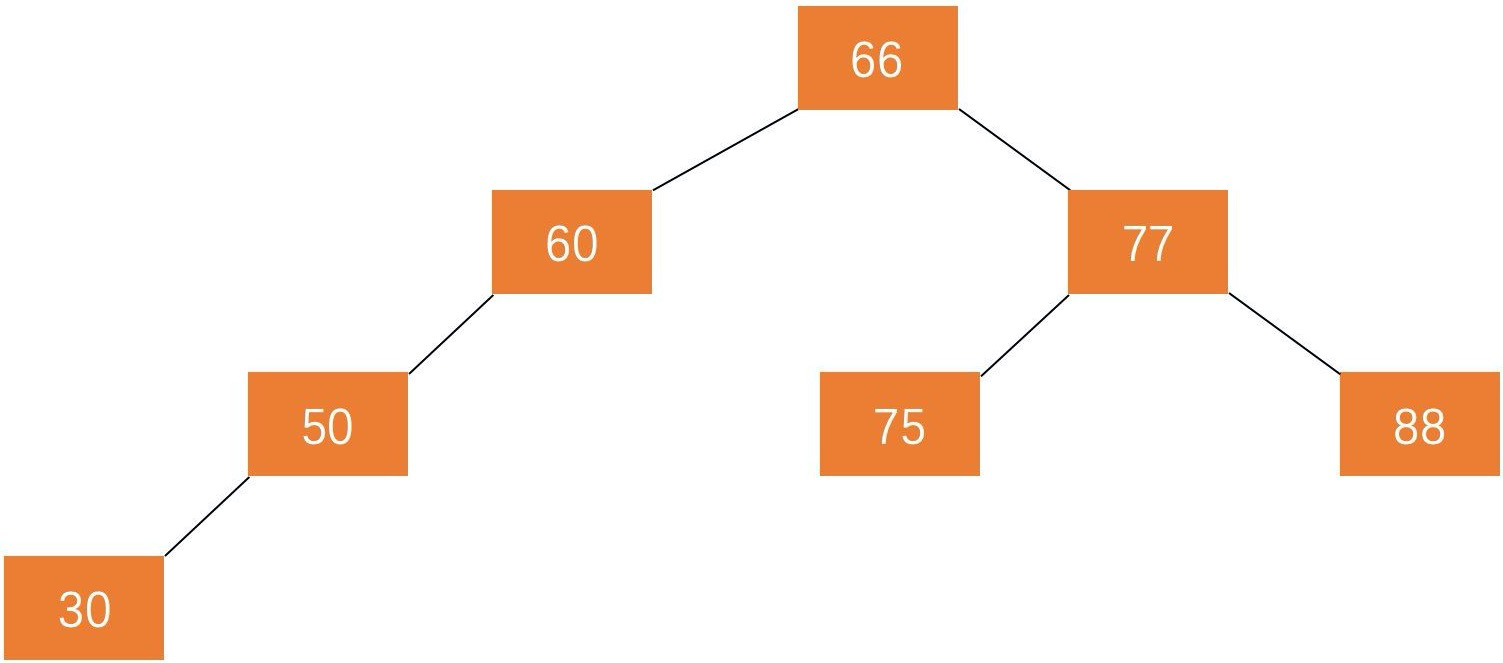
上图不是平衡二叉树，因为结点 60 的左子树不是平衡二叉树。


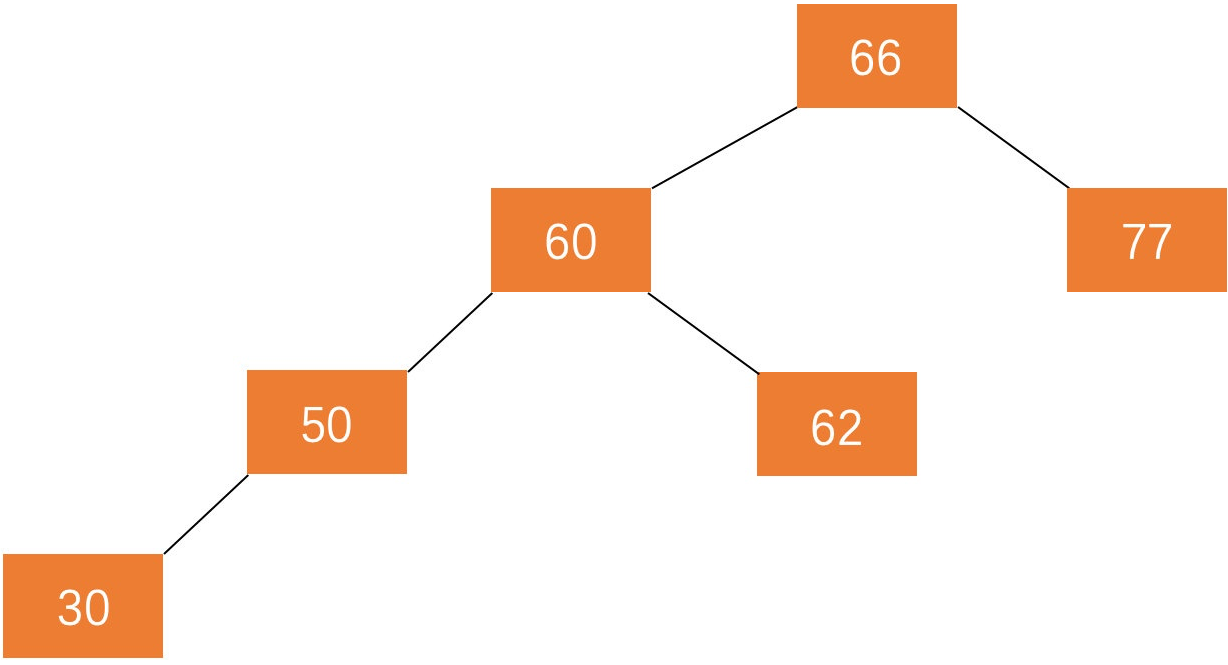
上图也不是平衡二叉树，因为虽然任何一个结点的左子树与右子树都是平衡二叉树，但高度之差已经超过 $1$。


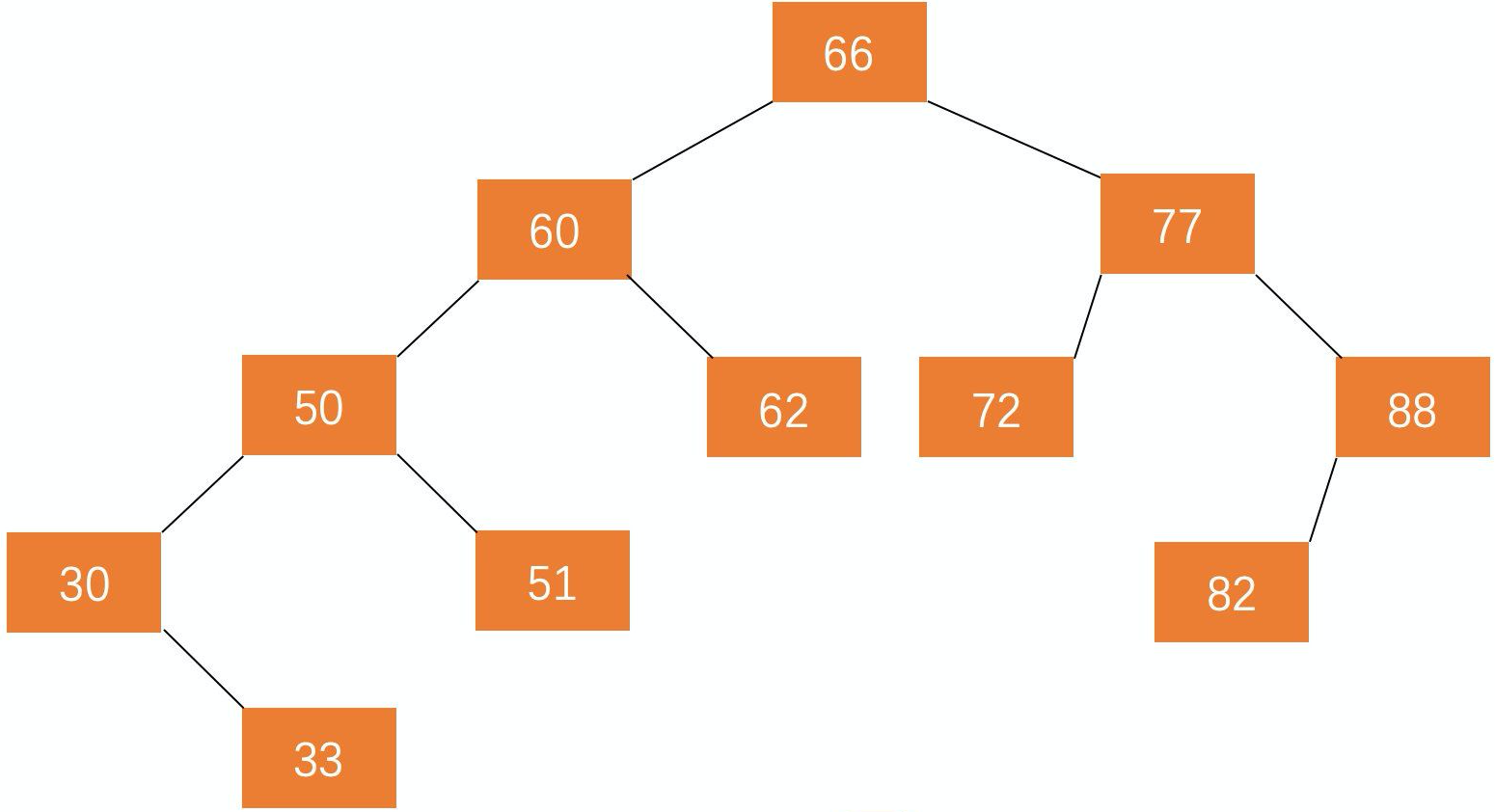
上图是 AVL。

【 AVL 插入时的失衡和调整】
如果在AVL树中进行插入或删除节点后，可能导致AVL树失去平衡。这种失去平衡的可以概括为4种姿态：LL(左左)，LR(左右)，RR(右右)和RL(右左)。下面给出它们的示意图：

上图中的 $4$ 棵树都是”失去平衡的AVL树”，从左往右的情况依次是：LL、LR、RL、RR。除了上面的情况之外，还有其它的失去平衡的AVL树，如下图：

AVL失去平衡之后，可以通过旋转使其恢复平衡，下面分别介绍”LL(左左)，LR(左右)，RR(右右)和RL(右左)”这 $4$ 种情况对应的旋转方法。


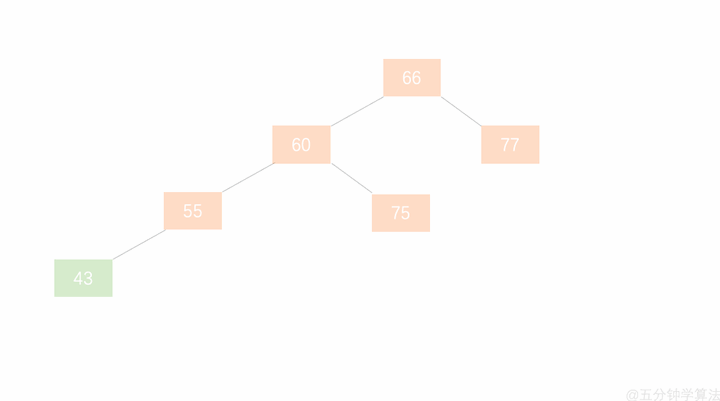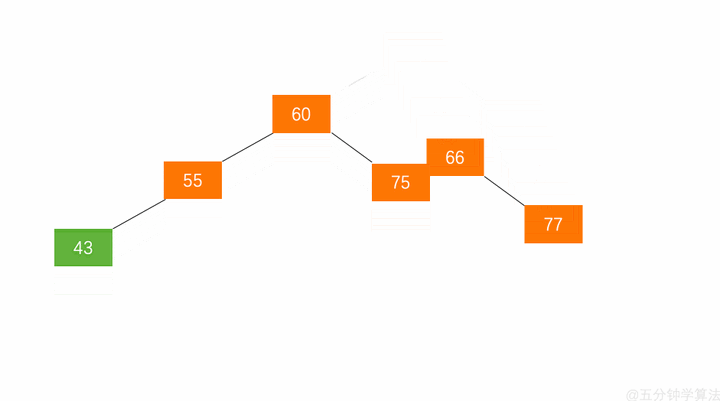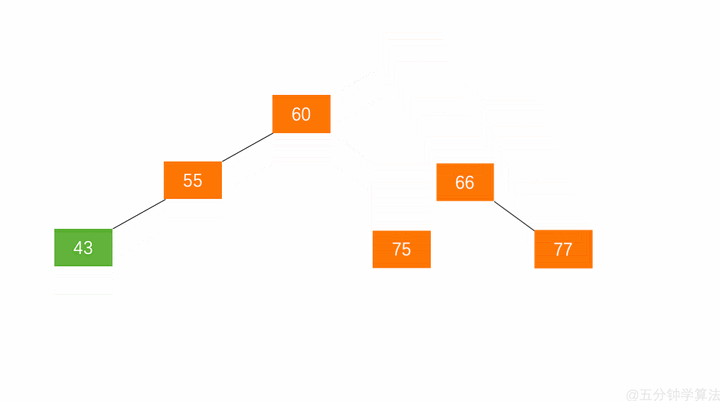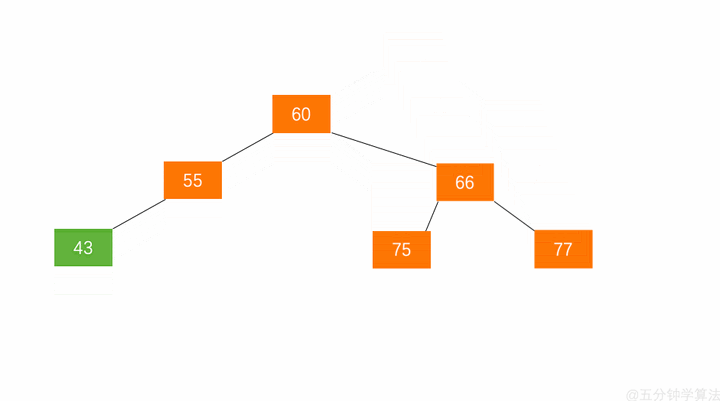
如上图在此平衡二叉树插入节点 99 ，树结构变为：

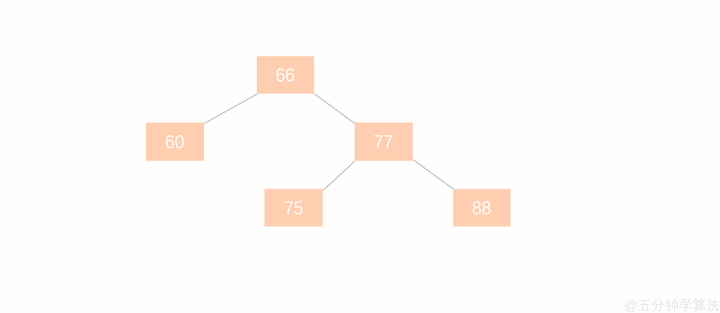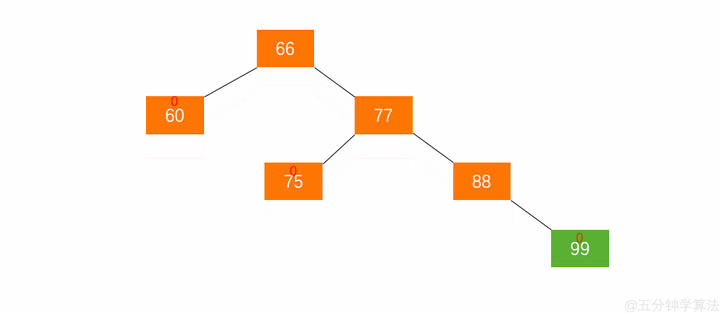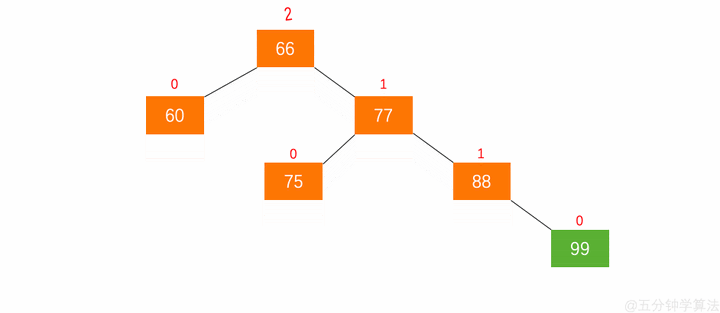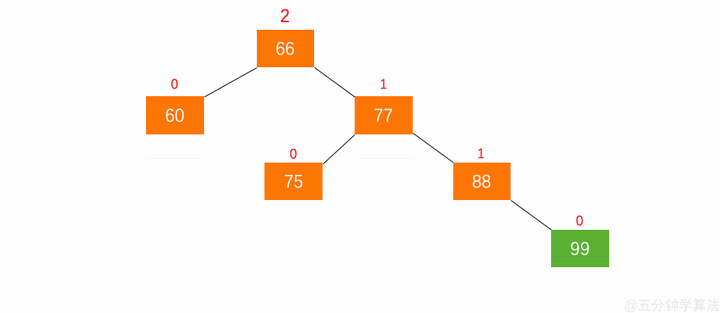
在动图中，节点 $66$ 的左子树高度为 $1$，右子树高度为 $3$，此时平衡因子为 $-2$，树失去平衡。

在动图中，以节点 $66$ 为父节点的那颗树就称为 最小失衡子树。
最小失衡子树：在新插入的结点向上查找，以第一个平衡因子的绝对值超过 1 的结点为根的子树称为最小不平衡子树。也就是说，一棵失衡的树，是有可能有多棵子树同时失衡的。而这个时候，我们只要调整最小的不平衡子树，就能够将不平衡的树调整为平衡的树。

平衡二叉树的失衡调整主要是通过旋转最小失衡子树来实现的。根据旋转的方向有两种处理方式，左旋 与 右旋 。

旋转的目的就是减少高度，通过降低整棵树的高度来平衡。哪边的树高，就把那边的树向上旋转。
【左旋】

LL失去平衡的情况，可以通过一次旋转让AVL树恢复平衡。如下图：

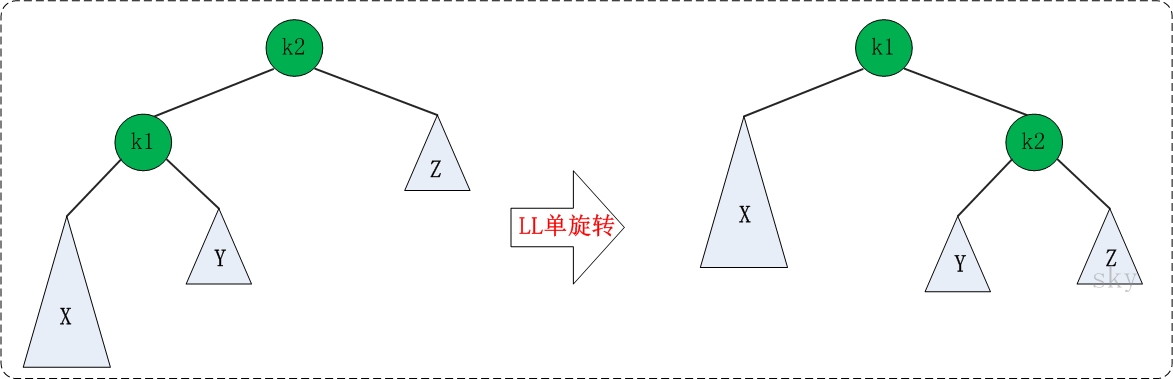
图中左边是旋转之前的树，右边是旋转之后的树。从中可以发现，旋转之后的树又变成了 AVL 树，而且该旋转只需要一次即可完成。
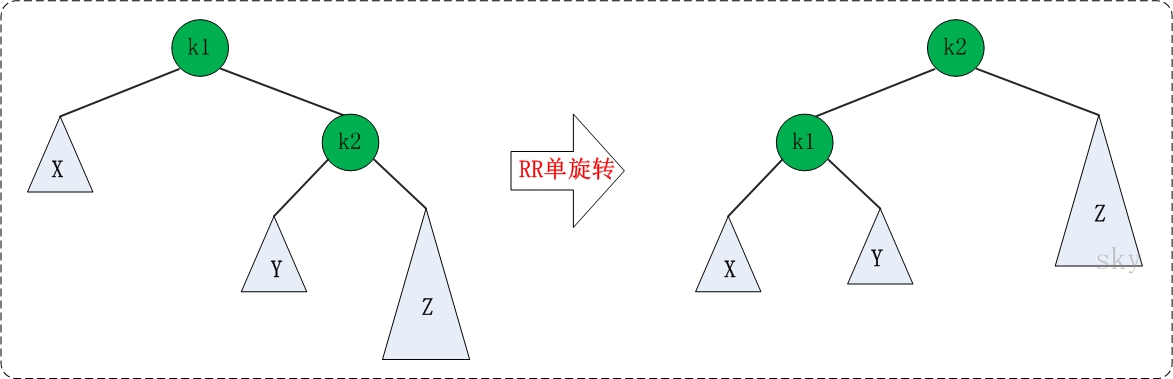
对于 LL 旋转，你可以这样理解为：LL 旋转是围绕”失去平衡的 AVL 根节点”进行的，也就是节点 k2；而且由于是 LL 情况，即左左情况，就用手抓着”左孩子，即 k1”使劲摇。将 k1 变成根节点，k2 变成 k1 的右子树，”k1 的右子树”变成” k2 的左子树”。

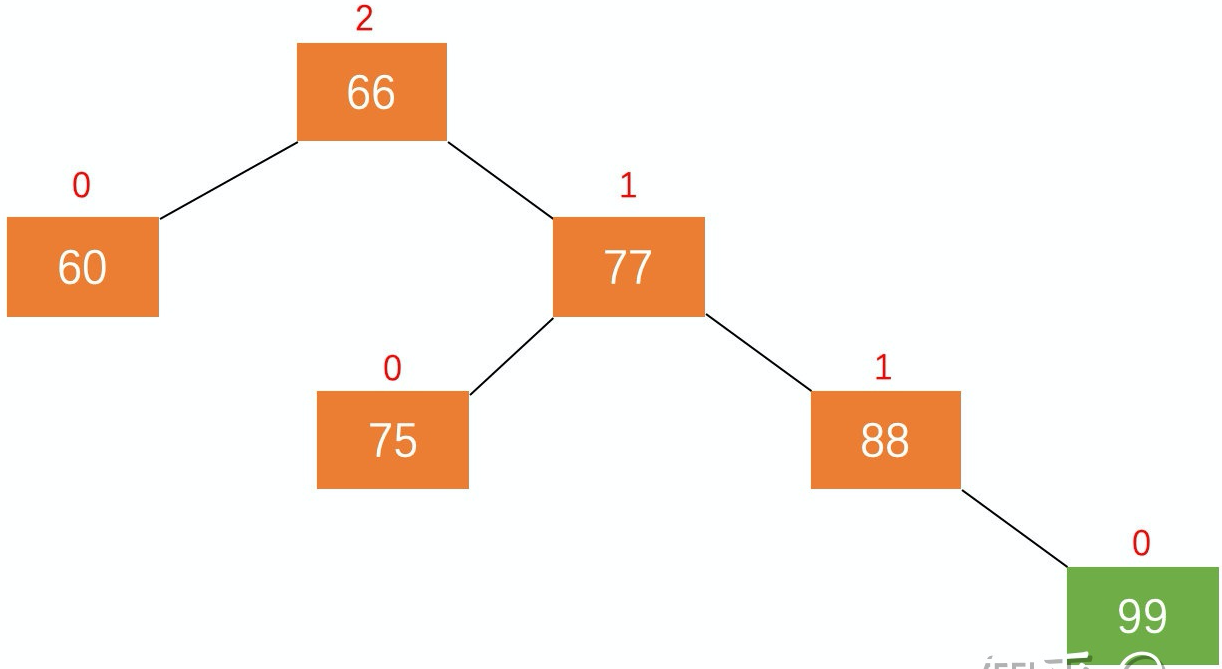
加入新节点 99 后， 节点 66 的左子树高度为 1，右子树高度为 3，此时平衡因子为 -2。为保证树的平衡，此时需要对节点 66 做出旋转，因为右子树高度高于左子树，对节点进行左旋操作，流程如下：

（1）节点的右孩子替代此节点位置 （2）右孩子的左子树变为该节点的右子树 （3）节点本身变为右孩子的左子树

整个操作流程如动图所示。

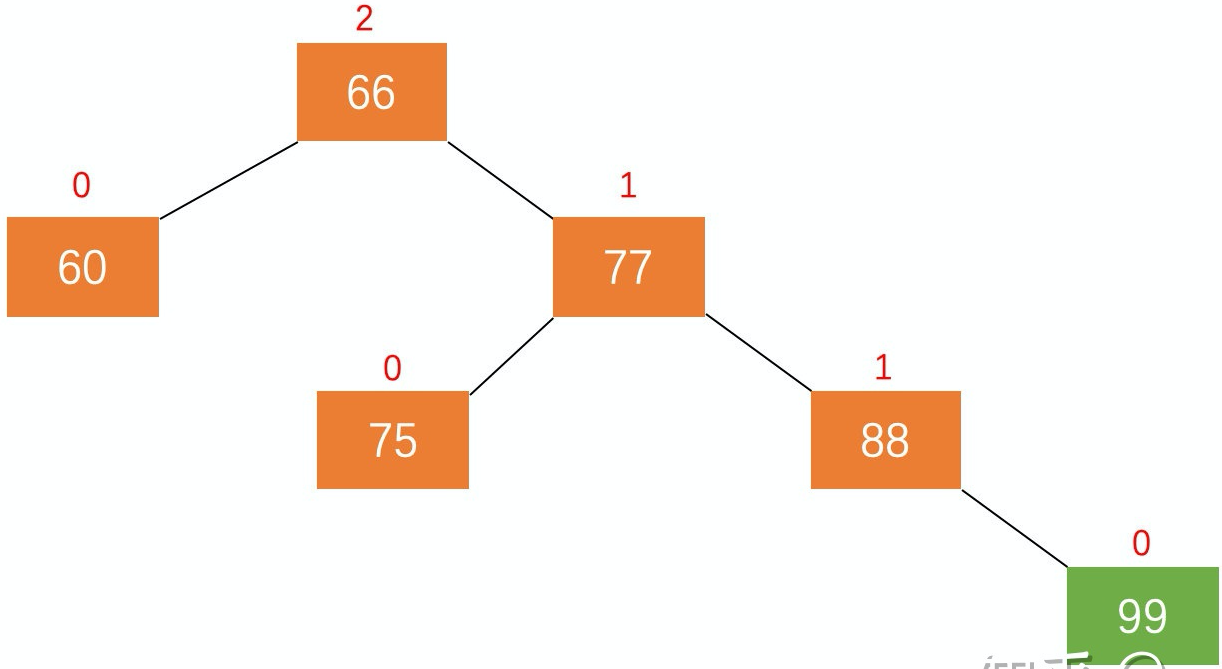
• 节点的右孩子替代此节点位置 —— 节点 $66$ 的右孩子是节点 $77$，将节点 $77$ 代替节点 $66$ 的位置
• 右孩子的左子树变为该节点的右子树 —— 节点 $77$ 的左子树为节点 $75$，将节点 $75$ 挪到节点 $66$ 的右子树位置
• 节点本身变为右孩子的左子树 —— 节点 $66$ 变为了节点 $77$ 的左子树

【右旋】

右旋操作与左旋类似，操作流程为：
（1）节点的左孩子代表此节点 （2）节点的左孩子的右子树变为节点的左子树 （3）将此节点作为左孩子节点的右子树。

【LR 旋转】

LR失去平衡的情况，需要经过两次旋转才能让AVL树恢复平衡。如下图：

【RL 旋转】

第一次旋转是围绕”k3”进行的”LL旋转”，第二次是围绕”k1”进行的”RR旋转”。

【左孩子的左子树插入节点（LL）】

只需要执行一次右旋即可。

【右孩子的右子树插入节点（RR）】

只需要执行一次左旋即可。

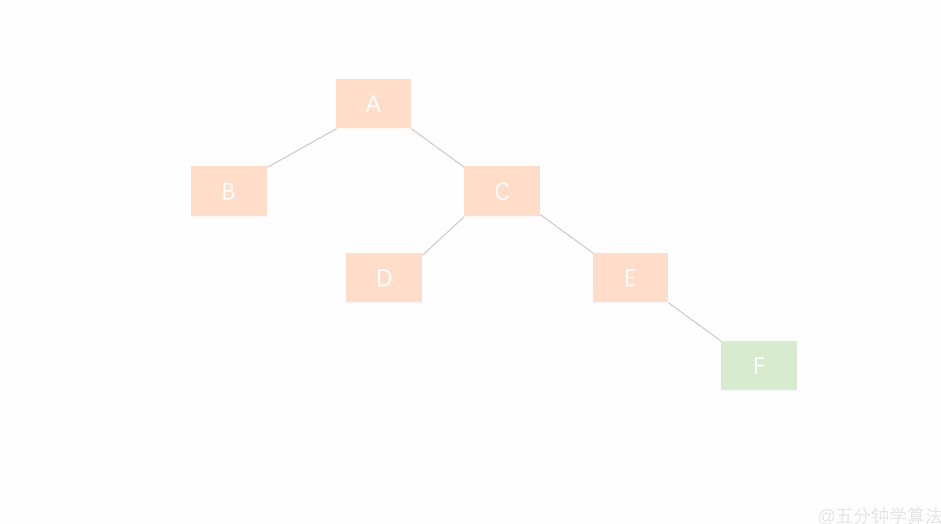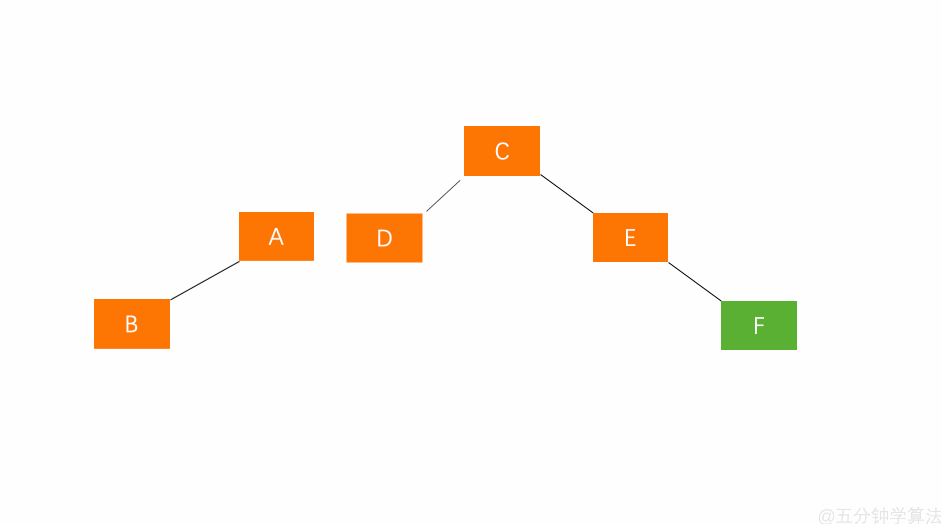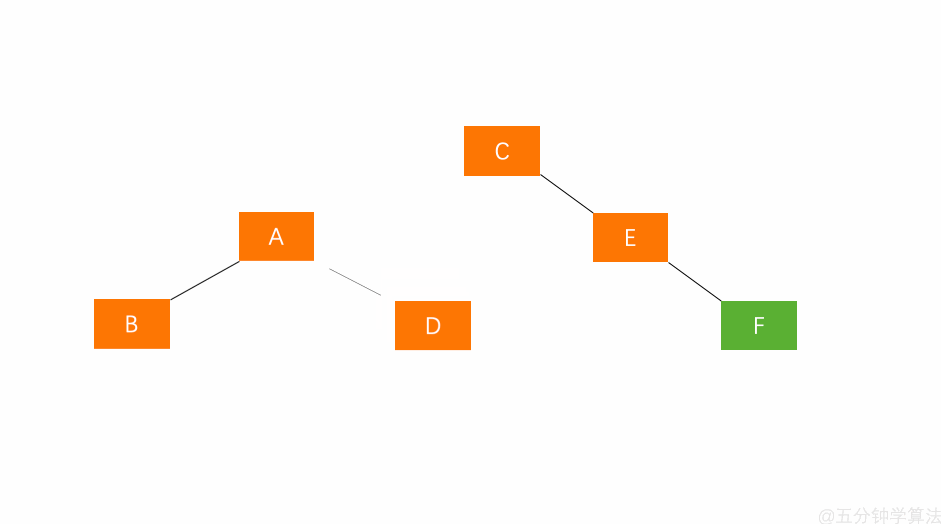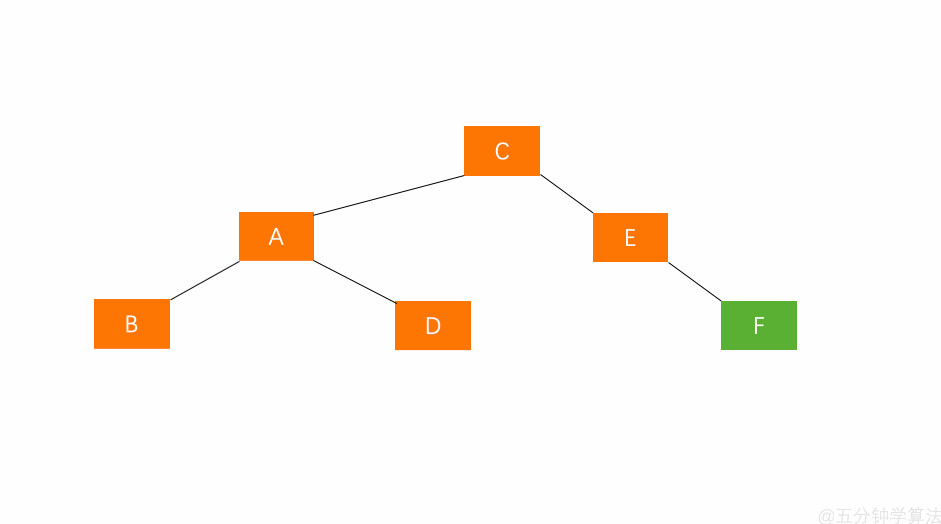
【左孩子的右子树插入节点（LR）】

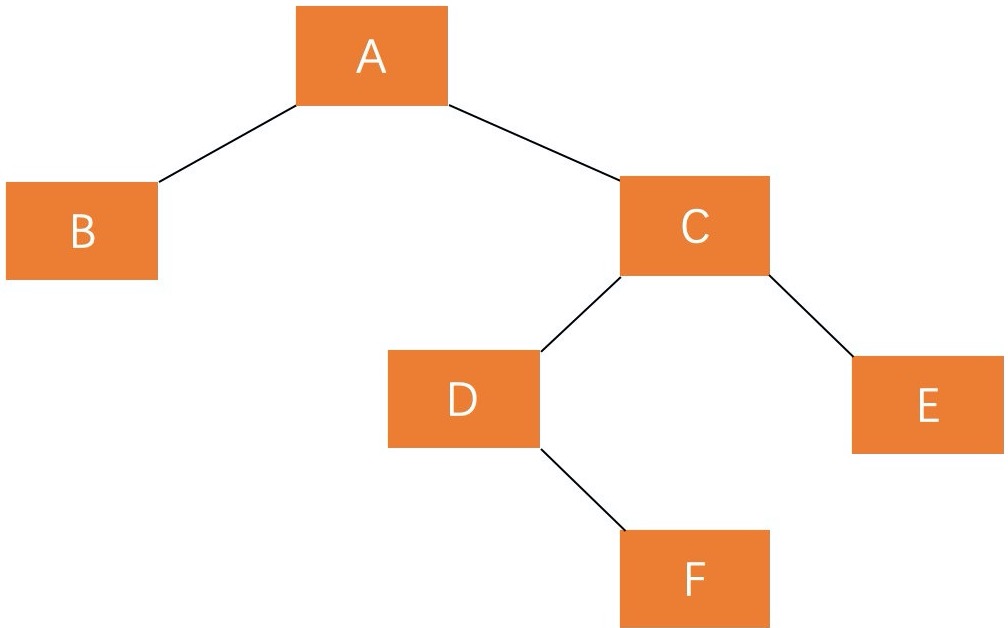
若 A 的左孩子节点 B 的右子树 E 插入节点 F ，导致节点 A 失衡，如图：

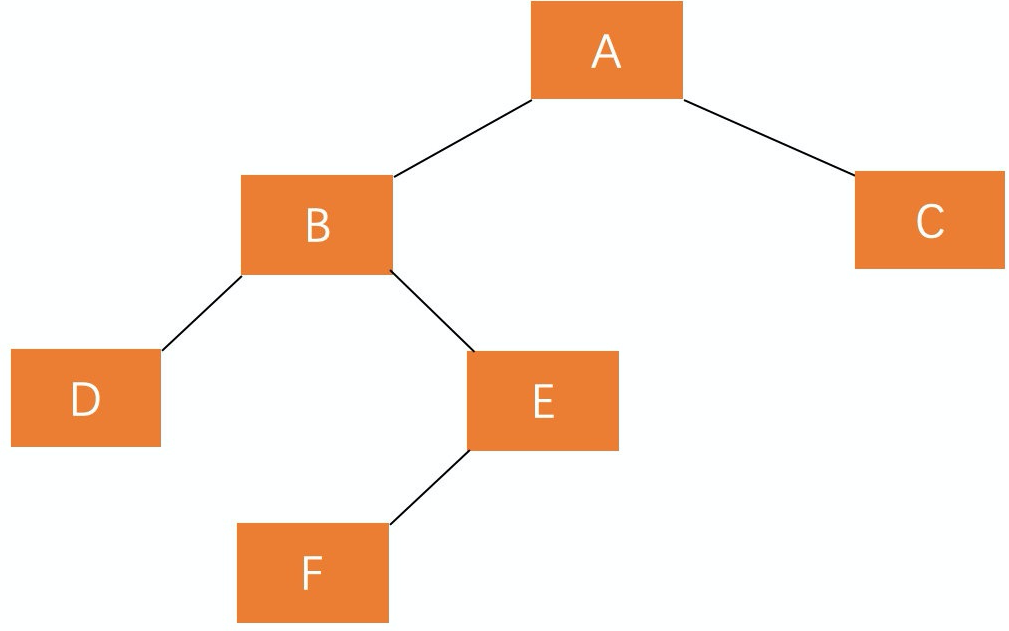
A 的平衡因子为 2，这种插入方式需要执行两步操作，使得旋转之后为 原来根结点的左孩子的右孩子作为新的根节点 。（1）对失衡节点 A 的左孩子 B 进行左旋操作，即上述 RR 情形操作。 （2）对失衡节点 A 做右旋操作，即上述 LL 情形操作。 调整过程如下：

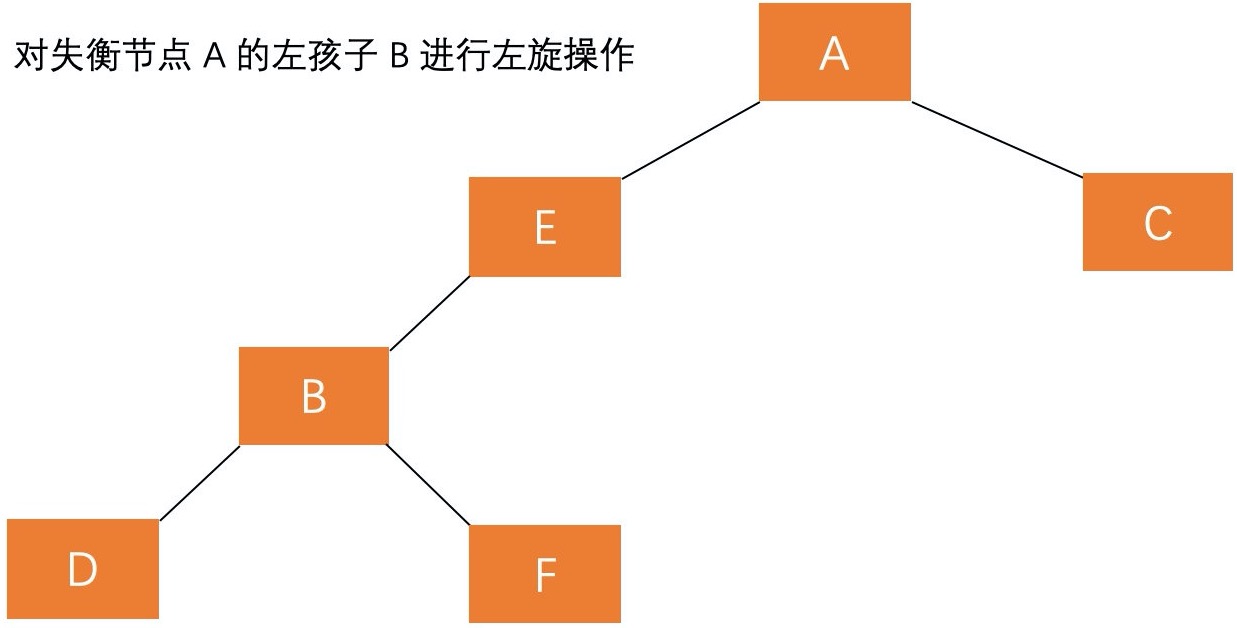
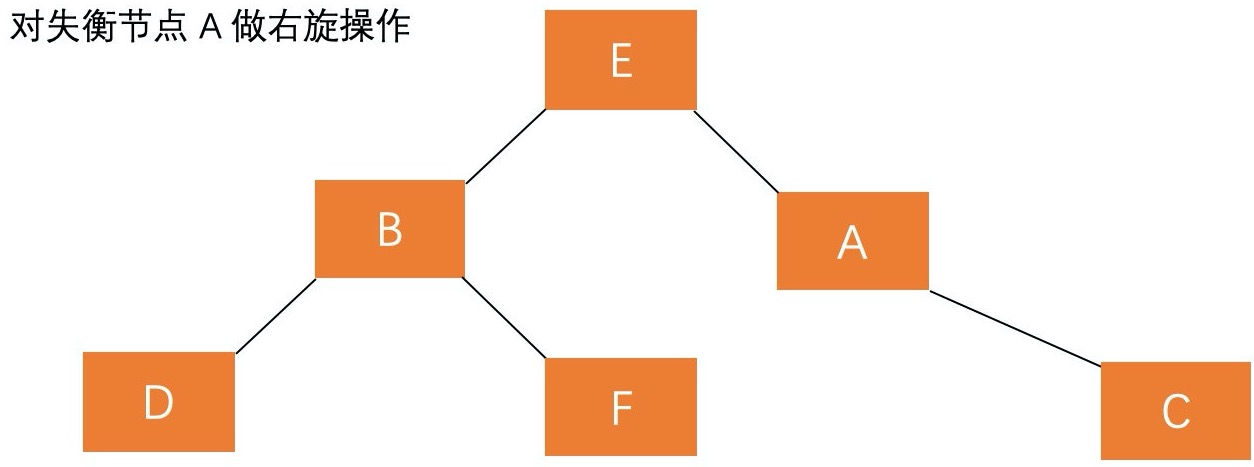
也就是说，经过这两步操作，使得 原来根节点的左孩子的右孩子 E 节点成为了新的根节点。

右孩子插入左节点的过程与左孩子插入右节点过程类似，也是需要执行两步操作，使得旋转之后为 原来根结点的右孩子的左孩子作为新的根节点 。
（1）对失衡节点 A 的右孩子 C 进行右旋操作，即上述 LL 情形操作。 （2）对失衡节点 A 做左旋操作，即上述 RR 情形操作。

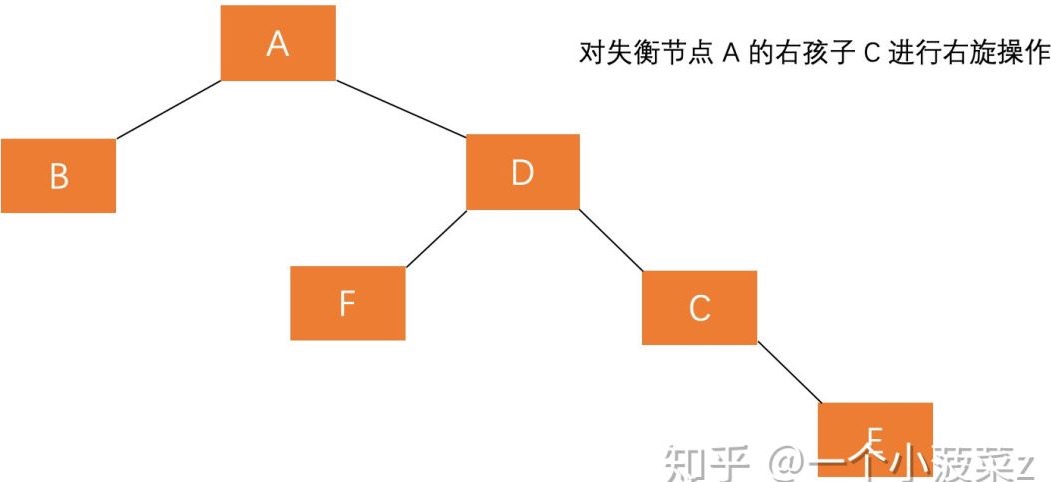
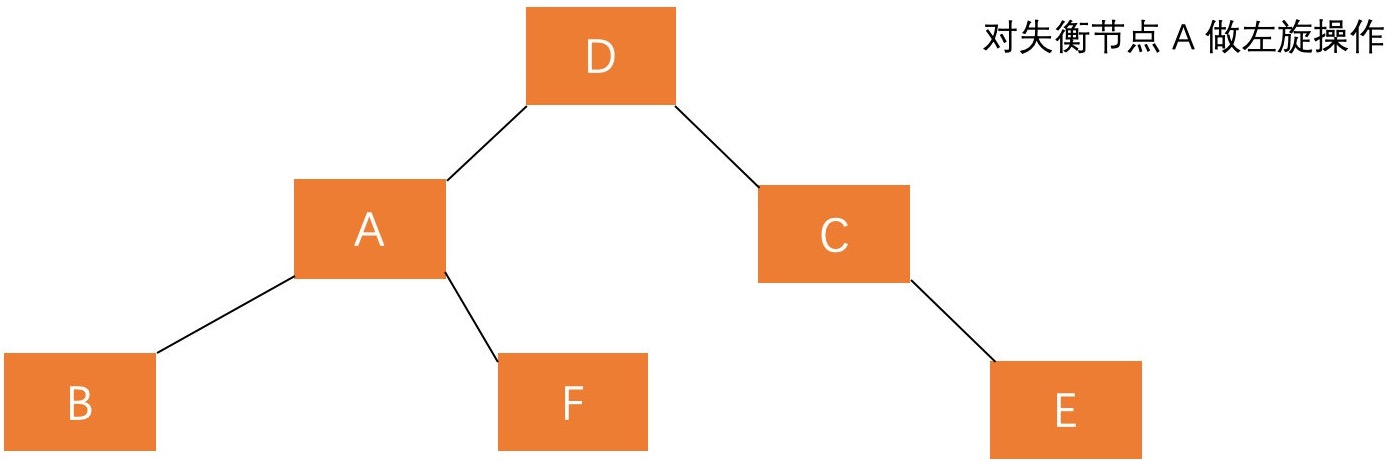
也就是说，经过这两步操作，使得 原来根节点的右孩子的左孩子 D 节点成为了新的根节点。

【代码实现】

可以使用 C++ 代码直接显示 AVL 树，当然这样代码量比较大。

也可以使用 STL 的优先队列来实现。方法是根据 AVL 的性质，维护一个大跟堆和小跟堆。

【使用 STL pbds 实现】

//包含两个头
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>

//引入命名空间
using namespace __gnu_pbds;

//定义AVL
tree<pii,null_type,less<pii>,rb_tree_tag,tree_order_statistics_node_update> tr;//红黑树

//插入操作
tr.insert({x,i+1});                 //插入x，用独特的正整数i+1标注（因为erase太辣鸡），因为 erase 是删除所有

//删除操作
t.erase(t.lower_bound({x,0}));     //删除x（删除单个元素）

//求排名，小于 x 的元素个数
t.order_of_key({x,0})+1;           //x的排名（小于x的元素个数+1）

//排名为x的元素
t.find_by_order(x-1)->first;       //排名为x的元素（第x小的数）

//x的前驱。即小于 x 的最大值
prev(t.lower_bound({x,0}))->first; //x的前驱（小于x且最大）

//x的后继。即大于 x 的最小值
t.lower_bound({x+1,0})->first;     //x的后继（大于x且最小）