如今的道路收费发展很快。道路的密度越来越大，因此选择最佳路径是很现实的问题。城市的道路是双向的，每条道路有固定的旅行时间以及需要支付的费用。
路径是连续经过的道路组成的。总时间是各条道路旅行时间的和，总费用是各条道路所支付费用的总和。一条路径越快，或者费用越低，该路径就越好。严格地说，如果一条路径比别的路径更快，而且不需要支付更多费用，它就比较好。反过来也如此理解。如果没有一条路径比某路径更好，则该路径被称为最小路径。
这样的最小的路径有可能不止一条，或者根本不存在路径。
问题：读入网络，计算最小路径的总数。费用时间都相同的两条最小路径只算作一条。你只要输出不同种类的最小路径数即可。

第一行有四个整数，城市总数 $n$，道路总数 $m$，起点和终点城市 $s,e$；
接下来的 $m$ 行每行描述了一条道路的信息，包括四个整数，两个端点 $p,r$，费用 $c$，以及时间 $t$；
两个城市之间可能有多条路径连接。

仅一个数，表示最小路径的总数。

对于全部数据，$1 \leq n \leq 100,\ 0 \leq m \leq 300,\ 1 \leq s,e,p,r \leq n,\ 0 \leq c,t \leq 100$，保证 $s \neq e,\ p \neq r$。

2

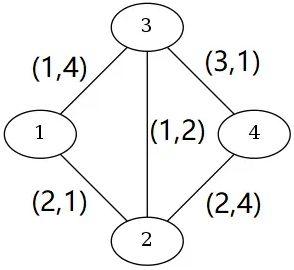
从 $1$ 到 $4$ 有 $4$ 条路径。为 $1 \to 2 \to 4$（费用为 $4$，时间为 $5$），$1 \to 3 \to 4$（费用为 $4$，时间为 $5$），$1 \to 2 \to 3 \to 4$（费用为 $6$，时间为 $4$），$1 \to 3 \to 2 \to 4$（费用为 $4$，时间为 $10$）。
$1 \to 3 \to 4$ 和 $1 \to 2 \to 4$ 比 $1 \to 3 \to 2 \to 4$ 更好。有两种最佳路径：费用为 $4$，时间为 $5$（$1 \to 2 \to 4$ 和 $1 \to 3 \to 4$）和费用为 $6$，时间为 $4$（$1 \to 2 \to 3 \to 4$）。