6491: 学习系列 —— 高斯消元(Gaussian elimination)
[Creator : ]
Description
【高斯消元】
是线性代数规划中的一个算法,可用来为线性方程组求解。
高斯消元的目标是将矩阵变为上三角矩阵,例如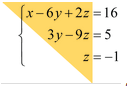 ,对应的矩阵为$\begin{bmatrix}
,对应的矩阵为$\begin{bmatrix}
1 & -6 & 2\\
0 & 3 & -9\\
0 & 0 & 1\end{bmatrix}$就是一个上三角矩阵(upper triangular matrix)。注意,在 C++ 中,我们可以使用二维数组来描述。
对于一个线性方程组 $\begin{cases}
a_1x+b_1y+c_1z=d_1\\
a_2x+b_2y+c_2z=d_2\\
a_3x+b_3y+c_3z=d_3\\
\end{cases}$,我们可以写出两个矩阵(系数矩阵(Coefficient Matrix)和增广矩阵(Augmented Matrix)),如下所示。
线性系统 系数矩阵 增广矩阵
$\begin{cases}
a_1x+b_1y+c_1z=d_1\\
a_2x+b_2y+c_2z=d_2\\
a_3x+b_3y+c_3z=d_3\\
\end{cases} \qquad\rightarrow
\begin{bmatrix}
a_1 & b_1 & c_1\\
a_2 & b_2 & c_2\\
a_3 & b_3 & c_3\end{bmatrix} \qquad \leftrightarrow
\begin{bmatrix}
a_1 & b_1 & c_1 & | & d_1\\
a_2 & b_2 & c_2 & | & d_2\\
a_3 & b_3 & c_3 & | & d_3\end{bmatrix}$
下面我们用一个图片简单的说明一下高斯消去。

当形成上图所示的上三角形状,我们可以非常简单的解出方程的解。这样的方法就是高斯消去法。
【高斯消元步骤】
高斯消去法的过程可以分为以下几步:
(一)、构造增广矩阵。即系数矩阵 A 加上常数向量 b,也就是 (A|b)。
(二)、通过以交换行、某行乘以非负常数和两行相加这三种初等变化将原系统转化为更简单的三角形式
(三)、得到简化的三角方阵组。
(四)、使用向后替换算法(Algorithm for Back Substitution)求解得。
方法一:原线性方程组 $rightarrow$ 高斯消元法 $rightarrow$ 上三角形式的线性方程组 $rightarrow$ 前向替换算法求解。
方法二:原线性方程组 $rightarrow$ 高斯消元法 $rightarrow$ 下三角形式的线性方程组 $rightarrow$ 后向替换算法求解。
【高斯消去细节】
顺序消去法虽然编程操作简单,但是存在以下两方面限制:
(1).每次运算时,必须保证对角线上的元素不为0(即运算中的分母不为0),否则算法无法继续进行。
(2).即使的值不为零,但如果绝对值很小,由于第k次运算中在分母位置,因此作除数会引起很大的误差,从而影响算法的稳定性。
正是由于顺序消去法会因为的值过小而引入计算误差,为了减少计算过程中舍入误差对方程组求解的影响,因此是否可以选择绝对值尽可能大的主元作为除数。基于这种思想就有了高斯消去法的改进型:部分主元消去法(Gaussian Elimination with Partial Pivoting)。
【Gaussian Elimination with Partial Pivoting】
下面我们使用一个详细的例子,来说明一下整个过程。假设我们有这样一个方程:
$\begin{cases}
0.02*x_1+0.01*x_2+0*x_3+0*x_4=0.02\\
1*x_1+2*x_2+1*x_3+0*x_4=1\\
0*x_1+1*x_2+2*x_3+1*x_4=4\\
0*x_1+0*x_2+100*x_3+200*x_4=800\\
\end{cases}$
我们可以得到对应的增广矩阵为 $\begin{bmatrix}
0.02 & 0.01 & 0 & 0 & | & 0.02\\
1 & 2 & 1 & 0 & | & 1\\
0 & 1 & 2 & 1 & | & 4\\
0 & 0 & 100 & 200 & | & 800\end{bmatrix}$,我们将使用列主元的方法。
Step 0a: 找主元。主元就是左边矩阵的第一列绝对值最大的数。
Step 0b: 如果需要,进行行交换,这样保证主元在第一行。
如上图所示的增广矩阵,第一列的主元为 1,因此我们需要进行行交换。交换后的矩阵如下图。

Step 1: 对第一列进行高斯消去,这样我们可以得到下图的增广矩阵。
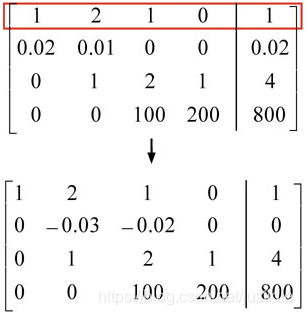
这样,我们就完成了第一列的高斯消去。
Step 2: 查找下一列(第二列)的主元。注意已经完成的列不需要参与。
Step 3: 交换行,如果需要。我们必须保证这个主元在这列的对角线位置。
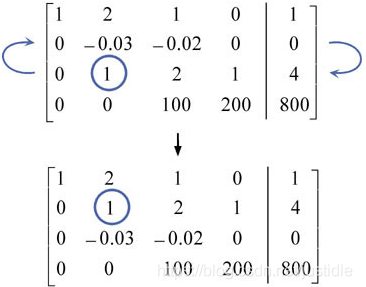
Step 4: 对第二列进行高斯消去,这样我们可以得到下图的增广矩阵。
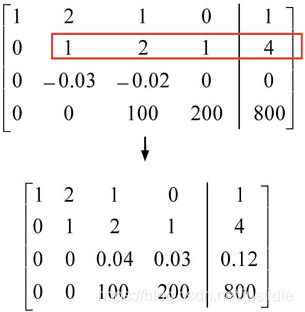
Step 5: 查找下一列(第三列)的主元。注意已经完成的列不需要参与。
Step 6: 交换行,如果需要。
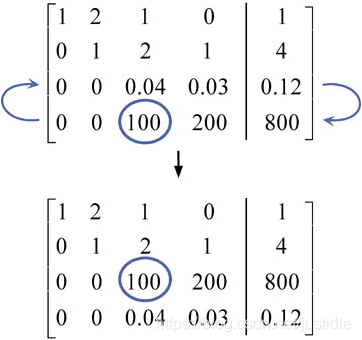
Step 7: 对第三列进行高斯消去,这样我们可以得到下图的增广矩阵。

Step 8: 到这里,我们就形成了上三角矩阵,下面我们用后向替换算法求解。
$\begin{cases}
-0.2*x_4=-0.05\\
100*x_3+200*x_4=800\\
x_2+2*x_3+x_4=4\\
x_1+2*x_2+x_3=1\\
\end{cases} \qquad \rightarrow \qquad \begin{cases}
x_4=4\\
x_3=0\\
x_2=0\\
x_1=1\\
\end{cases}$
利用主元法,我们可以消除舍入误差(rounding errors)。
是线性代数规划中的一个算法,可用来为线性方程组求解。
高斯消元的目标是将矩阵变为上三角矩阵,例如
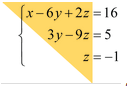 ,对应的矩阵为$\begin{bmatrix}
,对应的矩阵为$\begin{bmatrix} 1 & -6 & 2\\
0 & 3 & -9\\
0 & 0 & 1\end{bmatrix}$就是一个上三角矩阵(upper triangular matrix)。注意,在 C++ 中,我们可以使用二维数组来描述。
对于一个线性方程组 $\begin{cases}
a_1x+b_1y+c_1z=d_1\\
a_2x+b_2y+c_2z=d_2\\
a_3x+b_3y+c_3z=d_3\\
\end{cases}$,我们可以写出两个矩阵(系数矩阵(Coefficient Matrix)和增广矩阵(Augmented Matrix)),如下所示。
线性系统 系数矩阵 增广矩阵
$\begin{cases}
a_1x+b_1y+c_1z=d_1\\
a_2x+b_2y+c_2z=d_2\\
a_3x+b_3y+c_3z=d_3\\
\end{cases} \qquad\rightarrow
\begin{bmatrix}
a_1 & b_1 & c_1\\
a_2 & b_2 & c_2\\
a_3 & b_3 & c_3\end{bmatrix} \qquad \leftrightarrow
\begin{bmatrix}
a_1 & b_1 & c_1 & | & d_1\\
a_2 & b_2 & c_2 & | & d_2\\
a_3 & b_3 & c_3 & | & d_3\end{bmatrix}$
下面我们用一个图片简单的说明一下高斯消去。

当形成上图所示的上三角形状,我们可以非常简单的解出方程的解。这样的方法就是高斯消去法。
【高斯消元步骤】
高斯消去法的过程可以分为以下几步:
(一)、构造增广矩阵。即系数矩阵 A 加上常数向量 b,也就是 (A|b)。
(二)、通过以交换行、某行乘以非负常数和两行相加这三种初等变化将原系统转化为更简单的三角形式
(三)、得到简化的三角方阵组。
(四)、使用向后替换算法(Algorithm for Back Substitution)求解得。
方法一:原线性方程组 $rightarrow$ 高斯消元法 $rightarrow$ 上三角形式的线性方程组 $rightarrow$ 前向替换算法求解。
方法二:原线性方程组 $rightarrow$ 高斯消元法 $rightarrow$ 下三角形式的线性方程组 $rightarrow$ 后向替换算法求解。
【高斯消去细节】
顺序消去法虽然编程操作简单,但是存在以下两方面限制:
(1).每次运算时,必须保证对角线上的元素不为0(即运算中的分母不为0),否则算法无法继续进行。
(2).即使的值不为零,但如果绝对值很小,由于第k次运算中在分母位置,因此作除数会引起很大的误差,从而影响算法的稳定性。
正是由于顺序消去法会因为的值过小而引入计算误差,为了减少计算过程中舍入误差对方程组求解的影响,因此是否可以选择绝对值尽可能大的主元作为除数。基于这种思想就有了高斯消去法的改进型:部分主元消去法(Gaussian Elimination with Partial Pivoting)。
【Gaussian Elimination with Partial Pivoting】
下面我们使用一个详细的例子,来说明一下整个过程。假设我们有这样一个方程:
$\begin{cases}
0.02*x_1+0.01*x_2+0*x_3+0*x_4=0.02\\
1*x_1+2*x_2+1*x_3+0*x_4=1\\
0*x_1+1*x_2+2*x_3+1*x_4=4\\
0*x_1+0*x_2+100*x_3+200*x_4=800\\
\end{cases}$
我们可以得到对应的增广矩阵为 $\begin{bmatrix}
0.02 & 0.01 & 0 & 0 & | & 0.02\\
1 & 2 & 1 & 0 & | & 1\\
0 & 1 & 2 & 1 & | & 4\\
0 & 0 & 100 & 200 & | & 800\end{bmatrix}$,我们将使用列主元的方法。
Step 0a: 找主元。主元就是左边矩阵的第一列绝对值最大的数。
Step 0b: 如果需要,进行行交换,这样保证主元在第一行。
如上图所示的增广矩阵,第一列的主元为 1,因此我们需要进行行交换。交换后的矩阵如下图。

Step 1: 对第一列进行高斯消去,这样我们可以得到下图的增广矩阵。

这样,我们就完成了第一列的高斯消去。
Step 2: 查找下一列(第二列)的主元。注意已经完成的列不需要参与。
Step 3: 交换行,如果需要。我们必须保证这个主元在这列的对角线位置。

Step 4: 对第二列进行高斯消去,这样我们可以得到下图的增广矩阵。

Step 5: 查找下一列(第三列)的主元。注意已经完成的列不需要参与。
Step 6: 交换行,如果需要。

Step 7: 对第三列进行高斯消去,这样我们可以得到下图的增广矩阵。

Step 8: 到这里,我们就形成了上三角矩阵,下面我们用后向替换算法求解。
$\begin{cases}
-0.2*x_4=-0.05\\
100*x_3+200*x_4=800\\
x_2+2*x_3+x_4=4\\
x_1+2*x_2+x_3=1\\
\end{cases} \qquad \rightarrow \qquad \begin{cases}
x_4=4\\
x_3=0\\
x_2=0\\
x_1=1\\
\end{cases}$
利用主元法,我们可以消除舍入误差(rounding errors)。