6488: 学习系列 —— 字典(Trie)树
[Creator : ]
Description
【知识点】
字典树,英文名 Trie。又称单词查找树。
顾名思义,就是一个像字典一样的树。
字典树是高效的存储和查找字符串集合的数据结构。
字典树如下图。
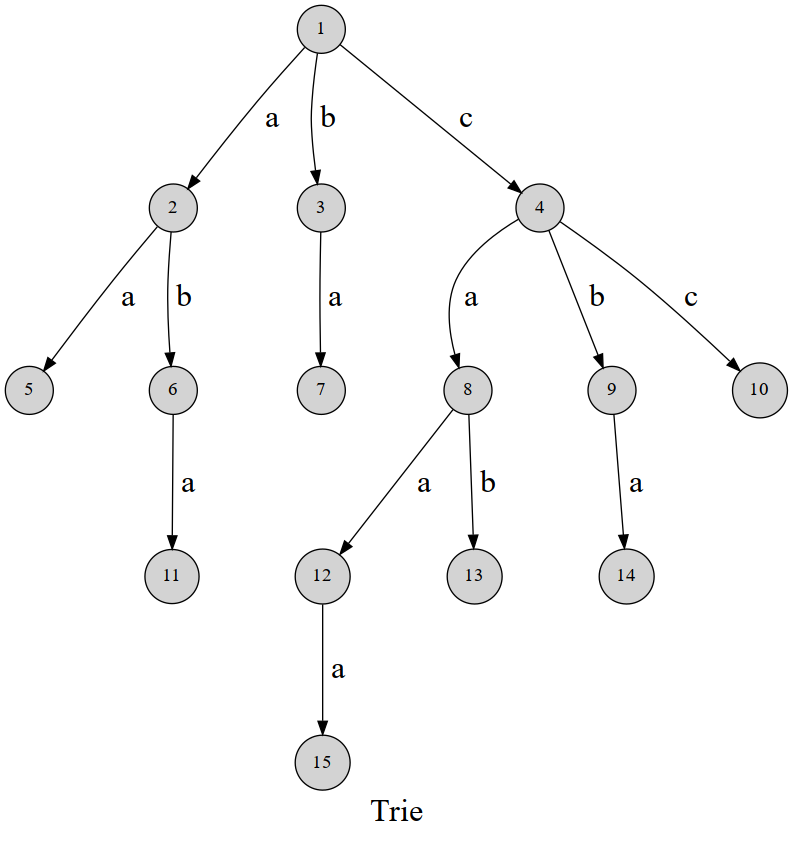
可以发现,这棵字典树用边来代表字母,而从根结点到树上某一结点的路径就代表了一个字符串。举个例子 $1->4->8->12$, 表示的就是字符串 caa。
Trie 的结构非常好懂,我们用 $\delta(u,\ c)$ 表示结点 $u$ 的 $c$ 字符指向的下一个结点,或着说是结点 $u$ 代表的字符串后面添加一个字符 $c$ 形成的字符串的结点。( $c$ 的取值范围和字符集大小有关,不一定是 $0 \sim 26$。)
有时需要标记插入进 Trie 的是哪些字符串,每次插入完成时在这个字符串所代表的节点处打上标记即可。比如我们要表示字典树中有单词 caa 存在,在对应的结点 $12$ 上打一个标志即可。
建立字典树,我们只需要实现两个函数:插入函数(insert)和询问函数(query)即可。
【字典树 MAXN】
【数据支持】
【将字符串 s 插入】
【查询字符串 s 出现的次数】
字典树,英文名 Trie。又称单词查找树。
顾名思义,就是一个像字典一样的树。
字典树是高效的存储和查找字符串集合的数据结构。
字典树如下图。

可以发现,这棵字典树用边来代表字母,而从根结点到树上某一结点的路径就代表了一个字符串。举个例子 $1->4->8->12$, 表示的就是字符串 caa。
Trie 的结构非常好懂,我们用 $\delta(u,\ c)$ 表示结点 $u$ 的 $c$ 字符指向的下一个结点,或着说是结点 $u$ 代表的字符串后面添加一个字符 $c$ 形成的字符串的结点。( $c$ 的取值范围和字符集大小有关,不一定是 $0 \sim 26$。)
有时需要标记插入进 Trie 的是哪些字符串,每次插入完成时在这个字符串所代表的节点处打上标记即可。比如我们要表示字典树中有单词 caa 存在,在对应的结点 $12$ 上打一个标志即可。
建立字典树,我们只需要实现两个函数:插入函数(insert)和询问函数(query)即可。
【字典树 MAXN】
假设节点的分支数为node_Branch,字符串数量为 $n$,字符串最大长度为 $\text(len)$,
那么最大节点数组= n * len
【数据支持】
const int MAXN=2e4+10;//根据题目定义 LL son[MAXN][30];//存放子节点 LL cnt[MAXN];//出现的次数统计 LL idx;//当前操作位置
【将字符串 s 插入】
void insert(const string &s) {
LL p=0;
for (LL i=0; i<s.size(); i++) {
LL t=s[i]-'a';
if (!son[p][t]) {
son[p][t]=++idx;
}
p=son[p][t];
}
//这里我们统计的是整个单词出现次数。如果是统计前缀,将这个部分放到循环内即可。
cnt[p]++;
}
【查询字符串 s 出现的次数】
LL query(const string &s) {
LL p=0;
for (LL i=0; i<s.size(); i++) {
LL t=s[i]-'a';
if (!son[p][t]) {
return 0;
}
p=son[p][t];
}
return cnt[p];
}
Input
【建树】
对字符串 e he her she shr son 组成的字典树如图所示。
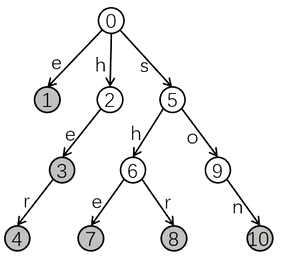
对字符串 e he her she shr son 组成的字典树如图所示。

const int N=1e6+10;
//TRIE相关数据定义
int trie[N][26];//Trie定义
int cnt[N];//cnt[i]表示第i个字符串的节点位置,即以i为终止节点的字符串出现的次数
int idx=0;//控制当前插入位置
//Trie树中插入字符串s
int insert(const std::string &s){
int p = 0;//插入位置
for (const auto &ch : s){
int c = ch - 'a';
if (!trie[p][c]) {
trie[p][c] = ++idx;
}
p = trie[p][c];
}
cnt[p]++;
return p;
}