6479: 学习系列 —— 图上 DFS
[Creator : ]
Description
其实就是在图(Graph)上进行 Deep First Search。
下面我们使用一个图来描述一下图上 DFS 过程。
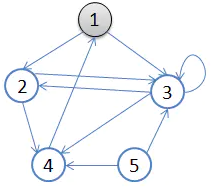
我们从顶点 $1$ 出发,遍历该图,注意 DFS 序可能不唯一。
我们首先访问顶点 $1$,将 $1$ 标注为黑色表示该顶点已经访问,这样图变为下图所示。
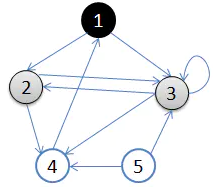
此时的 DFS 序为 $\{1\}$。
接着我们访问顶点 $1$ 的所有出边。我们首先选择顶点 $2$,访问顶点 $2$,这样图变为下图所示。
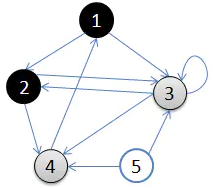
此时的 DFS 序为 $\{1,2\}$。
接着访问顶点 $2$ 的出边,这里我们选择顶点 $3$。这样图变为下图所示。
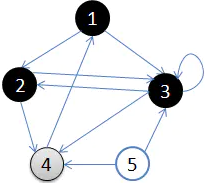
此时的 DFS 序为 $\{1,2,3\}$。
接着访问顶点 $3$ 的出边,这里我们选择顶点 $4$。这样图变为下图所示。
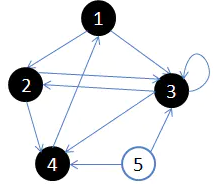
此时的 DFS 序为 $\{1,2,3,4\}$。
这样,我们就完成了对图的深度优先搜索。
得到一个从顶点 $1$ 出发的 DFS 序为 $\{1,2,3,4\}$。
注意:一个图的 DFS 序可能有多个,比如上图,另外一个合法的 DFS 序是 $\{1,3,4,2\}$。
【前置知识】
DFS 算法。
图的存储。需要掌握邻接矩阵,邻接表,能根据题目提供的数据范围,即 $n$ 的大小选择合适的方法。经验告诉我们当 $n$ 不超过 $2 \times 10^3$,我们可以优先考虑使用邻接矩阵(因为简单)。
【伪代码】
【复杂度】
时间复杂度为 $O(n+m)$。
空间复杂度为 $O(n)$。
下面我们使用一个图来描述一下图上 DFS 过程。

我们从顶点 $1$ 出发,遍历该图,注意 DFS 序可能不唯一。
我们首先访问顶点 $1$,将 $1$ 标注为黑色表示该顶点已经访问,这样图变为下图所示。

此时的 DFS 序为 $\{1\}$。
接着我们访问顶点 $1$ 的所有出边。我们首先选择顶点 $2$,访问顶点 $2$,这样图变为下图所示。

此时的 DFS 序为 $\{1,2\}$。
接着访问顶点 $2$ 的出边,这里我们选择顶点 $3$。这样图变为下图所示。

此时的 DFS 序为 $\{1,2,3\}$。
接着访问顶点 $3$ 的出边,这里我们选择顶点 $4$。这样图变为下图所示。

此时的 DFS 序为 $\{1,2,3,4\}$。
这样,我们就完成了对图的深度优先搜索。
得到一个从顶点 $1$ 出发的 DFS 序为 $\{1,2,3,4\}$。
注意:一个图的 DFS 序可能有多个,比如上图,另外一个合法的 DFS 序是 $\{1,3,4,2\}$。
【前置知识】
DFS 算法。
图的存储。需要掌握邻接矩阵,邻接表,能根据题目提供的数据范围,即 $n$ 的大小选择合适的方法。经验告诉我们当 $n$ 不超过 $2 \times 10^3$,我们可以优先考虑使用邻接矩阵(因为简单)。
【伪代码】
DFS(v) // v 可以是图中的一个顶点,也可以是抽象的概念,如 dp 状态等。
在 v 上打访问标记
for u in v 的相邻节点
if u 没有打过访问标记 then
DFS(u)
end
end
end
如果我们使用邻接矩阵 $g$ 来存储图,那么对应的基础代码为: /*
u 表示当前访问的顶点
fa 表示 u 的父亲
*/
void dfs(LL u, LL fa) {
//将顶点u设置已经访问
vis=true;
//遍历u的所有出边
for (LL j=1; j<=n; j++) {
//顶点 j 没有被访问,同时 u 到 j 有边
if (vis[j]==false && g[j]) {
dfs(v, u);
}
}
}
如果我们使用邻接表来存储图。那么对应的基础代码为 /*
u 表示当前访问的顶点
fa 表示 u 的父亲
*/
void dfs(LL u, LL fa) {
//将顶点u设置已经访问
vis=true;
//遍历u的所有出边
for (LL i=h; i!=-1; i=ne[i]) {
LL v=e[i];
//顶点 v 没有被访问,邻接表保证了 u 到 v 有边
if (vis[v]==false) {
dfs(v, u);
}
}
}
【复杂度】
时间复杂度为 $O(n+m)$。
空间复杂度为 $O(n)$。