6478: 学习系列 —— 二分图
[Creator : ]
Description
【二分图】
二分图,又称二部图,英文名叫 Bipartite graph。
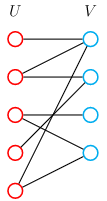
二分图是什么?节点由两个集合组成,且两个集合内部没有边的图。
换言之,存在一种方案,将节点划分成满足以上性质的两个集合。
【性质】
【匹配】
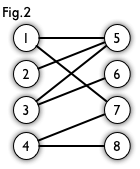
一个「匹配」(matching)是一个边的集合,其中任意两条边都没有公共顶点。例如,图 3、图 4 中红色的边就是图 2 的匹配。
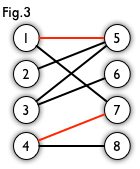
我们定义匹配点、匹配边、未匹配点、非匹配边,它们的含义非常显然。例如图 3 中 $1,4,5,7$ 为匹配点,其他顶点为未匹配点;$1 \ sim 5, 4 \sim 7$ 为匹配边,其他边为非匹配边。
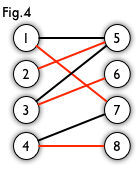
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。图 4 是一个最大匹配,它包含 $4$ 条匹配边。
完美匹配:如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配。图 4 是一个完美匹配。显然,完美匹配一定是最大匹配(完美匹配的任何一个点都已经匹配,添加一条新的匹配边一定会与已有的匹配边冲突)。但并非每个图都存在完美匹配。
举例来说:如下图所示,如果在某一对男孩和女孩之间存在相连的边,就意味着他们彼此喜欢。是否可能让所有男孩和女孩两两配对,使得每对儿都互相喜欢呢?图论中,这就是完美匹配问题。如果换一个说法:最多有多少互相喜欢的男孩/女孩可以配对儿?这就是最大匹配问题。

最大匹配数:最大匹配的匹配边的数目
最小点覆盖数:选取最少的点,使任意一条边至少有一个端点被选择
最大独立数:选取最多的点,使任意所选两点均不相连
最小路径覆盖数:对于一个 DAG(有向无环图),选取最少条路径,使得每个顶点属于且仅属于一条路径。路径长可以为 $0$(即单个点)。
定理1:最大匹配数 = 最小点覆盖数(这是 Konig 定理)
定理2:最大匹配数 = 最大独立数
定理3:最小路径覆盖数 = 顶点数 - 最大匹配数
【判定】
如何判定一个图是不是二分图呢?我们需要知道是否可以将图中的顶点分成两个满足条件的集合。
显然,直接枚举答案集合的话实在是太慢了,我们需要更高效的方法。
我们可以使用 DFS 或者 BFS 来遍历图。如果发现了奇环,那么就不是二分图,否则该图就是二分图。
【应用】
二分图最大匹配。
二分图最大权匹配。
一般图最大匹配。
一般图最大权匹配。
二分图,又称二部图,英文名叫 Bipartite graph。
二分图是什么?节点由两个集合组成,且两个集合内部没有边的图。
换言之,存在一种方案,将节点划分成满足以上性质的两个集合。

【性质】
-
如果两个集合中的点分别染成黑色和白色,可以发现二分图中的每一条边都一定是连接一个黑色点和一个白色点。
-
二分图不存在长度为奇数的环。因为每一条边都是从一个集合走到另外一个集合,只有走偶数次才可能回到同一个集合。
【匹配】
一个「匹配」(matching)是一个边的集合,其中任意两条边都没有公共顶点。例如,图 3、图 4 中红色的边就是图 2 的匹配。



我们定义匹配点、匹配边、未匹配点、非匹配边,它们的含义非常显然。例如图 3 中 $1,4,5,7$ 为匹配点,其他顶点为未匹配点;$1 \ sim 5, 4 \sim 7$ 为匹配边,其他边为非匹配边。
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。图 4 是一个最大匹配,它包含 $4$ 条匹配边。
完美匹配:如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配。图 4 是一个完美匹配。显然,完美匹配一定是最大匹配(完美匹配的任何一个点都已经匹配,添加一条新的匹配边一定会与已有的匹配边冲突)。但并非每个图都存在完美匹配。
举例来说:如下图所示,如果在某一对男孩和女孩之间存在相连的边,就意味着他们彼此喜欢。是否可能让所有男孩和女孩两两配对,使得每对儿都互相喜欢呢?图论中,这就是完美匹配问题。如果换一个说法:最多有多少互相喜欢的男孩/女孩可以配对儿?这就是最大匹配问题。

最大匹配数:最大匹配的匹配边的数目
最小点覆盖数:选取最少的点,使任意一条边至少有一个端点被选择
最大独立数:选取最多的点,使任意所选两点均不相连
最小路径覆盖数:对于一个 DAG(有向无环图),选取最少条路径,使得每个顶点属于且仅属于一条路径。路径长可以为 $0$(即单个点)。
定理1:最大匹配数 = 最小点覆盖数(这是 Konig 定理)
定理2:最大匹配数 = 最大独立数
定理3:最小路径覆盖数 = 顶点数 - 最大匹配数
【判定】
如何判定一个图是不是二分图呢?我们需要知道是否可以将图中的顶点分成两个满足条件的集合。
显然,直接枚举答案集合的话实在是太慢了,我们需要更高效的方法。
我们可以使用 DFS 或者 BFS 来遍历图。如果发现了奇环,那么就不是二分图,否则该图就是二分图。
【应用】
二分图最大匹配。
二分图最大权匹配。
一般图最大匹配。
一般图最大权匹配。