弗洛伊德（Floyd）算法是解决任意两点间的最短路径的一种算法，可以正确处理有向图或有向图或负权（但不可存在负权回路）的最短路径问题，同时也被用于计算有向图的传递闭包。
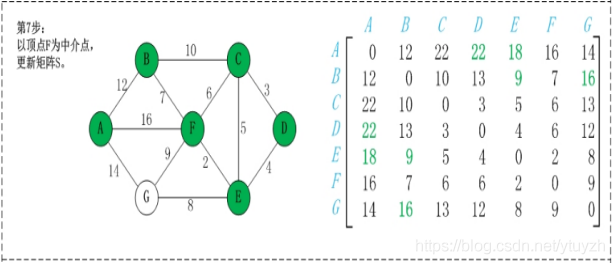
Floyd算法是一个经典的动态规划算法。
从任意节点 $i$ 到任意节点 $j$ 的最短路径不外乎 $2$ 种可能，一是直接从 $i \to j$，二是从 $i$ 经过节点 $k$ 到 $j$。所以，我们假设 $Dis(i,j)$ 为节点 $i$ 到节点 $j$ 的最短路径的距离，对于每一个节点 $k$，我们检查 $Dis(i,k) + Dis(k,j) < Dis(i,j)$ 是否成立，如果成立，证明从 $i$ 到 $k$ 再到 $j$ 的路径比 $i$ 直接到 $j$ 的路径短，我们便设置 $Dis(i,j) = Dis(i,k) + Dis(k,j)$，这样一来，当我们遍历完所有节点 $k$，$Dis(i,j)$ 中记录的便是i到j的最短路径的距离。
【时间复杂度】
$O(n^3)$。
【图的存储】
使用邻接矩阵。