6457: 树的 DFS II
[Creator : ]
Description
给定一棵 $n$ 个节点的树。
节点的编号为 $1 \sim n$,其中 $1$ 号节点为根节点,每个节点的编号都大于其父节点的编号。
请输出该树的 DFS 序,我们规定,当遍历(或回溯)到某一节点时,下一个遍历的目标应该是它的未经遍历的子节点中编号最小的那一个子节点。
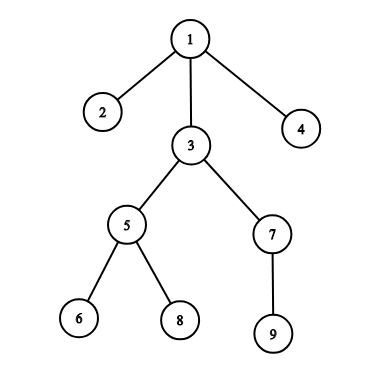
例如,上图实例中:
每个询问就是让你计算采用规定的 DFS 算法来遍历根节点为 $u_i$ 的子树。
节点的编号为 $1 \sim n$,其中 $1$ 号节点为根节点,每个节点的编号都大于其父节点的编号。
请输出该树的 DFS 序,我们规定,当遍历(或回溯)到某一节点时,下一个遍历的目标应该是它的未经遍历的子节点中编号最小的那一个子节点。

例如,上图实例中:
- 如果遍历根节点为 $1$ 号节点的子树,则子树内各节点的遍历顺序为 $[1,2,3,5,6,8,7,9,4]$。
- 如果遍历根节点为 $3$ 号节点的子树,则子树内各节点的遍历顺序为 $[3,5,6,8,7,9]$。
- 如果遍历根节点为 $7$ 号节点的子树,则子树内各节点的遍历顺序为 $[7,9]$。
- 如果遍历根节点为 $9$ 号节点的子树,则子树内各节点的遍历顺序为 $[9]$。
每个询问就是让你计算采用规定的 DFS 算法来遍历根节点为 $u_i$ 的子树。
Input
第一行包含两个整数 $n,q$。
第二行包含 $n−1$ 个整数 $p_2,p_3,…,p_n$,其中 $p_i$ 表示第 $i$ 号节点的父节点的编号。
接下来 $q$ 行,每行包含一个整数 $u_i$,表示一组询问。
第二行包含 $n−1$ 个整数 $p_2,p_3,…,p_n$,其中 $p_i$ 表示第 $i$ 号节点的父节点的编号。
接下来 $q$ 行,每行包含一个整数 $u_i$,表示一组询问。
Output
共 $q$ 行,每组询问输出一行若干个整数表示以 $u_i$ 为跟的子树 DFS 序。
Constraints
前三个测试点满足 $2≤n≤2000,\ 1≤q≤2000$。
所有测试点满足 $2≤n≤2×10^5,\ 1≤q≤2×10^5,\ 1≤p_i<i,\ 1≤u_i≤n$。
所有测试点满足 $2≤n≤2×10^5,\ 1≤q≤2×10^5,\ 1≤p_i<i,\ 1≤u_i≤n$。
Sample 1 Input
9 9
1 1 1 3 5 3 5 7
3
1
2
4
7
6
9
8
5
Sample 1 Output
3 5 6 8 7 9
1 2 3 5 6 8 7 9 4
2
4
7 9
6
9
8
5 6 8