6455: 学习系列 —— 图论:SPFA
[Creator : ]
Description
shortest path fastest algorithm 单源最短路问题求解算法之一。
【适用范围】
1、能求解带负权边的最短路径。
2、可以判断图中是否有环。
3、大部分情况下,SPFA 也可以求解正权图。而且速度比迪杰斯特拉算法更快。
4、但是大家请注意能使用迪杰斯特拉算法的时候,尽量使用迪杰斯特拉算法,以免碰到出题人卡 SPFA 的情况。注意万恶的出题人可能会卡 SPFA。
【时间复杂度】
最坏情况下:$O(mn)$。
SPFA总的期望时间复杂度为:$O(nlognlog(m/n) + m)$。
【算法步骤】
求下图起点 a 到所有点的最短路径。

Step 1:建立起点到所有点距离。
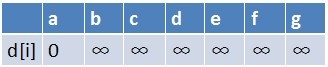
Step 2:我们使用普通队列对算法进行优化。将起点 a 推入队列。此时队列内有元素 {a}。
Step 3:当队列不空,将队首推出队列,并对该顶点所有出边进行松弛操作,直到队列为空。
具体的最短路更新过程如下。
队首元素 a 出队,对以 a 为起始点的所有边的终点依次进行松弛操作(此处有 b,c,d 三个点),此时路径表格状态为:
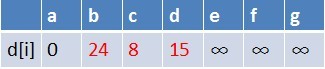
在松弛时三个点的最短路径估值变小了,而这些点队列中都没有出现,这些点需要入队,此时,队列中新入队了三个结点 {b,c,d}。
队首元素 b 点出队,对以 b 为起始点的所有边的终点依次进行松弛操作(此处只有 e 点),此时路径表格状态为:
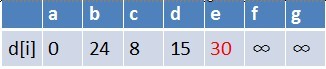
在最短路径表中,e 的最短路径估值也变小了,e 在队列中不存在,因此 e 也要入队,此时队列中的元素为 {c,d,e}。
队首元素 c 点出队,对以 c 为起始点的所有边的终点依次进行松弛操作(此处有 e,f 两个点),此时路径表格状态为:
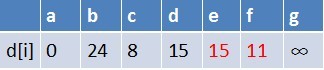
在最短路径表中,e,f 的最短路径估值变小了,e 在队列中存在,f 不存在。因此 e 不用入队了,f 要入队,此时队列中的元素为 {d,e,f}。
队首元素 d 点出队,对以 d 为起始点的所有边的终点依次进行松弛操作(此处只有 g 这个点),此时路径表格状态为:
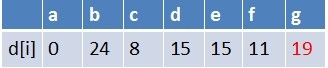
在最短路径表中,g 的最短路径估值变小了,g 在队列中不存在。因此 g 要入队,此时队列中的元素为 {e,f,g}。
队首元素 e 点出队,对以 e 为起始点的所有边的终点依次进行松弛操作(此处只有 g 这个点)。在最短路径表中,g 的最短路径估值没有变小(松弛不成功),没有新结点入队,队列中元素为 {f,g}。
队首元素 f 点出队,对以 f 为起始点的所有边的终点依次进行松弛操作(此处有 d,e,g 三个点),此时路径表格状态为:
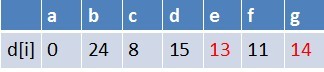
在最短路径表中,e,g 的最短路径估值又变小,队列中无 e 点,e 入队,队列中存在 g 这个点,g 不用入队,此时队列中元素为 {g,e}。
队首元素 g 点出队,对以 g 为起始点的所有边的终点依次进行松弛操作(此处只有 b 点),此时路径表格状态为:
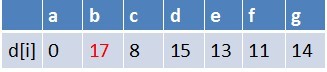
在最短路径表中,b 的最短路径估值又变小,队列中无 b 点,b 入队,此时队列中元素为 {e,b}。
队首元素 e 点出队,对以 e 为起始点的所有边的终点依次进行松弛操作(此处只有 g 这个点),此时路径表格状态为:
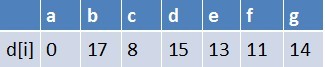
在最短路径表中,g 的最短路径估值没变化(松弛不成功),此时队列中元素为 {b}。
队首元素 b 点出队,对以 b 为起始点的所有边的终点依次进行松弛操作(此处只有 e 这个点),此时路径表格状态为:
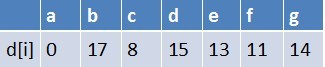
在最短路径表中,e 的最短路径估值没变化(松弛不成功),此时队列为空了,算法结束。
【算法模板】
数据存储我们使用单链表形式。
注意:使用本模板前,需要将 h 数组初始化为 $-1$。
【SPFA 求最短路】
【SPFA 判环】
使用 SPFA 判断图上第 $i$ 个顶点作为起点是否是否有环,可以在标准的 SPFA 算法上增加一个数组变量 cnt 表示第 $i$ 个顶点的最短路径包含的边数即可。
我们需要在算法中,先将需要判断环的节点加入到队列中。下面的模板是判断 $1 \sim n$ 作为起点是否构成环。
【适用范围】
1、能求解带负权边的最短路径。
2、可以判断图中是否有环。
3、大部分情况下,SPFA 也可以求解正权图。而且速度比迪杰斯特拉算法更快。
4、但是大家请注意能使用迪杰斯特拉算法的时候,尽量使用迪杰斯特拉算法,以免碰到出题人卡 SPFA 的情况。注意万恶的出题人可能会卡 SPFA。
【时间复杂度】
最坏情况下:$O(mn)$。
SPFA总的期望时间复杂度为:$O(nlognlog(m/n) + m)$。
【算法步骤】
求下图起点 a 到所有点的最短路径。

Step 1:建立起点到所有点距离。

Step 2:我们使用普通队列对算法进行优化。将起点 a 推入队列。此时队列内有元素 {a}。
Step 3:当队列不空,将队首推出队列,并对该顶点所有出边进行松弛操作,直到队列为空。
具体的最短路更新过程如下。
队首元素 a 出队,对以 a 为起始点的所有边的终点依次进行松弛操作(此处有 b,c,d 三个点),此时路径表格状态为:

在松弛时三个点的最短路径估值变小了,而这些点队列中都没有出现,这些点需要入队,此时,队列中新入队了三个结点 {b,c,d}。
队首元素 b 点出队,对以 b 为起始点的所有边的终点依次进行松弛操作(此处只有 e 点),此时路径表格状态为:

在最短路径表中,e 的最短路径估值也变小了,e 在队列中不存在,因此 e 也要入队,此时队列中的元素为 {c,d,e}。
队首元素 c 点出队,对以 c 为起始点的所有边的终点依次进行松弛操作(此处有 e,f 两个点),此时路径表格状态为:

在最短路径表中,e,f 的最短路径估值变小了,e 在队列中存在,f 不存在。因此 e 不用入队了,f 要入队,此时队列中的元素为 {d,e,f}。
队首元素 d 点出队,对以 d 为起始点的所有边的终点依次进行松弛操作(此处只有 g 这个点),此时路径表格状态为:

在最短路径表中,g 的最短路径估值变小了,g 在队列中不存在。因此 g 要入队,此时队列中的元素为 {e,f,g}。
队首元素 e 点出队,对以 e 为起始点的所有边的终点依次进行松弛操作(此处只有 g 这个点)。在最短路径表中,g 的最短路径估值没有变小(松弛不成功),没有新结点入队,队列中元素为 {f,g}。
队首元素 f 点出队,对以 f 为起始点的所有边的终点依次进行松弛操作(此处有 d,e,g 三个点),此时路径表格状态为:

在最短路径表中,e,g 的最短路径估值又变小,队列中无 e 点,e 入队,队列中存在 g 这个点,g 不用入队,此时队列中元素为 {g,e}。
队首元素 g 点出队,对以 g 为起始点的所有边的终点依次进行松弛操作(此处只有 b 点),此时路径表格状态为:

在最短路径表中,b 的最短路径估值又变小,队列中无 b 点,b 入队,此时队列中元素为 {e,b}。
队首元素 e 点出队,对以 e 为起始点的所有边的终点依次进行松弛操作(此处只有 g 这个点),此时路径表格状态为:

在最短路径表中,g 的最短路径估值没变化(松弛不成功),此时队列中元素为 {b}。
队首元素 b 点出队,对以 b 为起始点的所有边的终点依次进行松弛操作(此处只有 e 这个点),此时路径表格状态为:

在最短路径表中,e 的最短路径估值没变化(松弛不成功),此时队列为空了,算法结束。
【算法模板】
数据存储我们使用单链表形式。
注意:使用本模板前,需要将 h 数组初始化为 $-1$。
【SPFA 求最短路】
const LL INF=0x3f3f3f3f3f3f3f3f;
//顶点数据
const int N=1e5+10;
LL dis[N];
bool vis[N];
LL h[N];
//边数据
const int M=2e6+10;
LL e[M], w[M], ne[M], idx;
void spfa(LL st) {
//初始化距离
memset(dis, 0x3f, sizeof dis);
//处理起点
dis[st]=0;
vis[st]=true;
queue<LL> que;
que.push(st);
while (que.size()) {
LL u=que.front();
que.pop();
vis=false;
//对u的所有出边进行松弛
for (LL i=h; i!=-1; i++) {
LL v=e[i];
if (dis[v]>dis+w[i]) {
dis[v]=dis+w[i];
if (vis[v]==false) {
que.push(v);
vis[v]=true;
}
}
}
}
}
【SPFA 判环】
使用 SPFA 判断图上第 $i$ 个顶点作为起点是否是否有环,可以在标准的 SPFA 算法上增加一个数组变量 cnt 表示第 $i$ 个顶点的最短路径包含的边数即可。
我们需要在算法中,先将需要判断环的节点加入到队列中。下面的模板是判断 $1 \sim n$ 作为起点是否构成环。
bool spfa(LL st) {
//初始化距离
memset(dis, 0x3f, sizeof dis);
//处理起点
dis[st]=0; vis[st]=true;
queue<LL> que;
//下面操作将需要判环的顶点加入队列
for (LL i=1; i<=n; i++) { que.push(i); vis[i]=true; }
while (que.size()) {
LL u=que.front();
que.pop();
vis=false;
//对u的所有出边进行松弛
for (LL i=h; i!=-1; i++) {
LL v=e[i];
if (dis[v]>dis+w[i]) {
dis[v]=dis+w[i];
cnt[v]=cnt+1;
if (cnt[v]>n) { //已经包含了n条边,有环
return true;
}
if (vis[v]==false) { que.push(v); vis[v]=true; }
}
}
}
return false;//不存在环
}