6454: 学习系列 —— 图论:Bellman-Ford 算法
[Creator : ]
Description
是单源最短路问题求救算法之一。
【适用范围】
1、能求解带负权边的最短路径。但是在竞赛中,碰到负权图,我们一般使用 SPFA 算法,因为大部分情况下 SPFA 速度更快。
2、可以判断图中是否有环。但是一般使用 SPFA 算法。
3、碰到只能经过 $m$ 条边组成的最短路问题,就只能使用本算法解决。
【时间复杂度】
存在 $|V|$ 次对边集合的迭代松弛,边集合的大小为 $|E|$,所以Bellman-Ford 算法的时间复杂度为 $O(|V||E|)$。
【实现思想】
其实现方式是通过 $m$ 次迭代求出从源点到终点不超过 $m$ 条边构成的最短路的路径。很重要的一点是每次迭代都是在上一次的基础上进行的,因此我们在代码实现时要注意保留上一次的结果,在上一次的基础上算。
【图解过程】

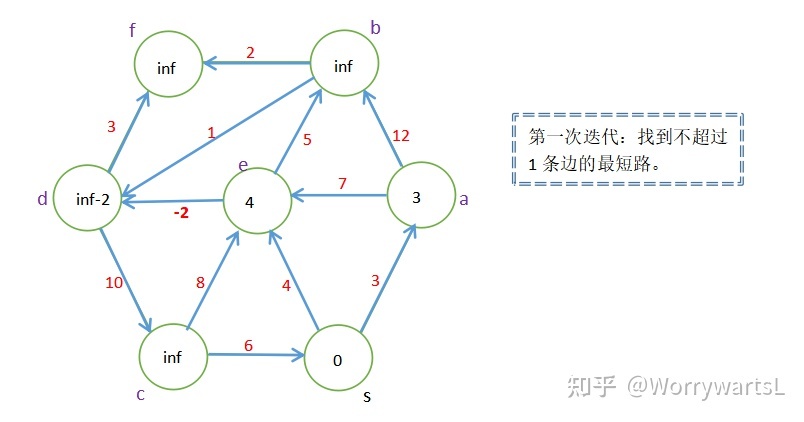
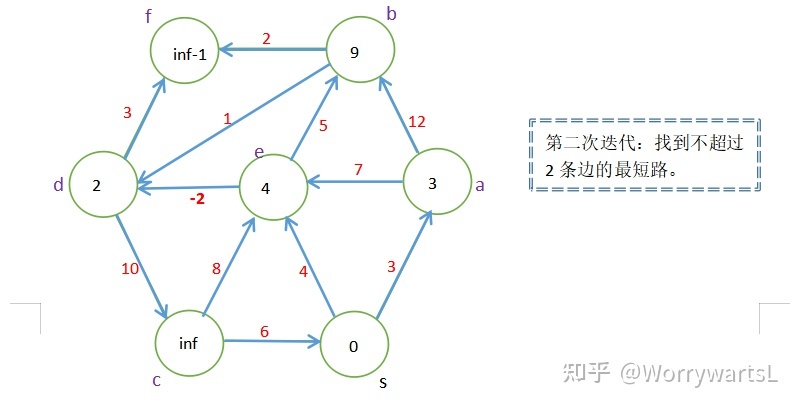
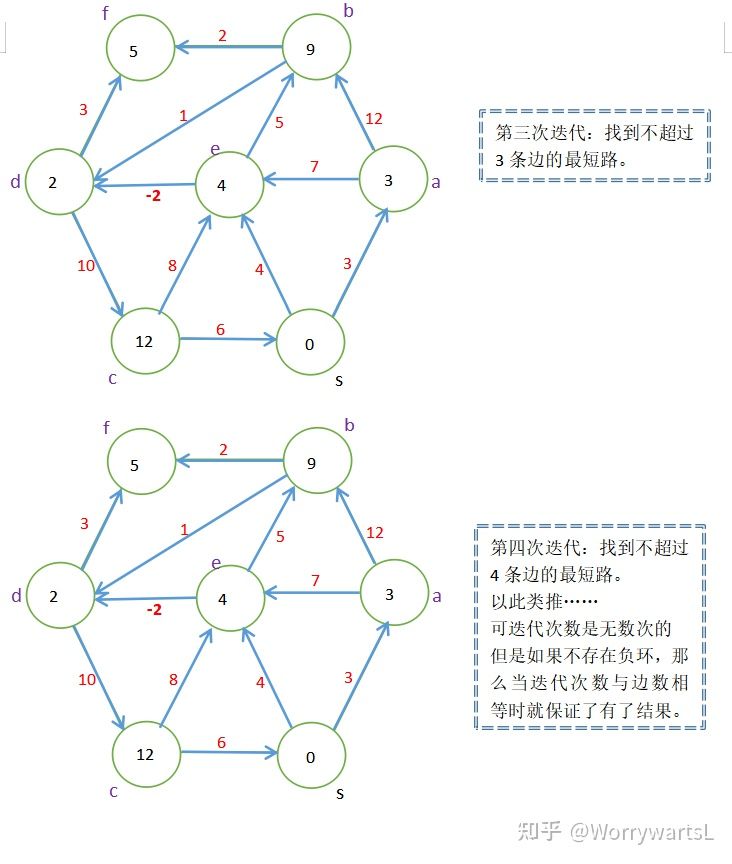
【实现细节】
1. 图存储使用链式前向星方式,存储每一条边。
2. 在本次松弛操作的时候,务必使用上一轮的数据。
【模板代码】
【适用范围】
1、能求解带负权边的最短路径。但是在竞赛中,碰到负权图,我们一般使用 SPFA 算法,因为大部分情况下 SPFA 速度更快。
2、可以判断图中是否有环。但是一般使用 SPFA 算法。
3、碰到只能经过 $m$ 条边组成的最短路问题,就只能使用本算法解决。
【时间复杂度】
存在 $|V|$ 次对边集合的迭代松弛,边集合的大小为 $|E|$,所以Bellman-Ford 算法的时间复杂度为 $O(|V||E|)$。
【实现思想】
其实现方式是通过 $m$ 次迭代求出从源点到终点不超过 $m$ 条边构成的最短路的路径。很重要的一点是每次迭代都是在上一次的基础上进行的,因此我们在代码实现时要注意保留上一次的结果,在上一次的基础上算。
【图解过程】




【实现细节】
1. 图存储使用链式前向星方式,存储每一条边。
2. 在本次松弛操作的时候,务必使用上一轮的数据。
【模板代码】
const LL INF=0x3f3f3f3f3f3f3f3f;
//顶点相关数据
const int N=1e3+10;
LL dis[N];//距离
LL backup[N];//上一轮距离
//保存所有的边
const int M=1e3+10;
struct EDGE {
LL u,v,w;
} a[M];
LL K;//最多包含K条边
LL m;//边的数量
//st 是起点
void bellman-ford(LL st) {
memset(dis, 0x3f, sizeof dis);//将距离设置为无穷大
dis[st]=0;
for (LL i=1; i<=K; i++) {
//通过这个实现使用上一轮数据进行迭代
memcpy(backup, dis, sizeof dis);
//遍历所有边进行迭代
for (LL i=1; i<=m; i++) {
//u->v w
LL u=a[j].u;
LL v=a[j].v;
LL w=a[j].w;
if (dis[v]>backup+w) {
dis[v]=backup+w;
}
}
}
//下面是判断无穷大,因为可能有负权边
if (dis[n]>=INF/2) {
//这里是无穷大
}