有一棵包含 $n$ 个节点和 $n-1$ 条边的树，规定树链 $(u,v)$ 为树上从 $u$ 到 $v$ 的简单路径。
树的每条边上都有一个正整数，这个正整数被称作这条边的颜色，规定一条树链的权值 $w(u,v)$ 为这条树链上所有边的颜色的代数和。
而整棵树的权值为所有不同的树链的权值的代数和。
已知所有边的颜色集合恰好为 $1$ 到 $n-1$ 这 $n-1$ 个不同的正整数，请你为每条边安排一种颜色，使得这棵树的权值尽量小，你不需要给出具体方案，只需要求出这个最小的权值即可。

测试数据第一行，是一个正整数 $n\ (1 \le n \le 10^5)$，表示树的节点个数。
接下来 $n-1$ 行，每行两个用空格隔开的整数 $u,v$，表示树上有一条边连接 $u$ 和 $v$。

一个整数，表示了这棵树的最小的权值。

19

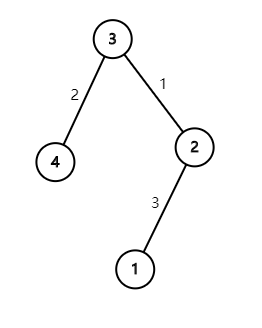
$w(1,2)+w(1,3)+w(1,4)+w(2,3)+w(2,4)+w(3,4)=3+4+6+1+3+2=19$。