我们把一个城市考虑为一个图，街道为边，路口为点。
路口标记为 $0 \sim N-1$，盗贼从一个点开始逃亡，每一分钟走一条边。不幸的是，我们并不知道他逃往何处，只能假设他每分钟都必须沿着一条边走，不能停留但是可以反复经过。
警官想要知道是否存在一个时刻，盗贼可能出现在城市中的任意路口。

第一行，一个整数 $T$，表示测试用例数。
每例第一行包含 $3$ 个整数，点数 $N,M,S$，其中 $N$ 表示路口 $N \leq 10^5$，边数 $M \leq 5*10^5$，起点 $S$。
接下来 $M$ 行，每行两个数字表示一条边。

如果存在这样的时刻输出"YES"，否则"NO"。
具体参看样例输出。

Case 1: YES
Case 2: NO

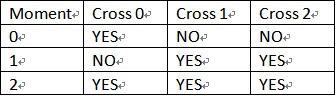
第 $1$ 个用例，入下图，YES 表示盗贼在某个时刻会出现在某个路口。