【迪杰斯特拉算法】
迪杰斯特拉算法干的事情是：给定一个有向图，有向图的各个边都是正数，指定一个源点，求出源点到其余各个节点的最短距离。
迪杰斯特拉算法采用的是一种贪心的策略。
【使用条件】
迪杰斯特拉算法适用于求正权图。图中可以有环，但不能有负权边。例如：下图就不能使用本算法来求。

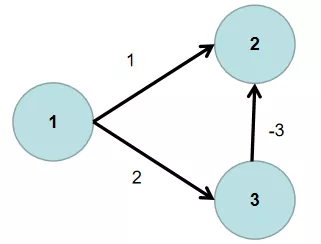
【步骤】
我们将图中各个节点用数字 $1 \sim n$ 编号，源点的编号为 $1$。

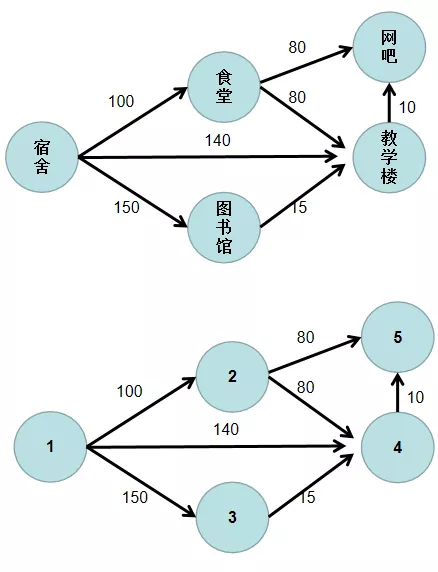
求源点到其余各点的最短距离步骤如下：
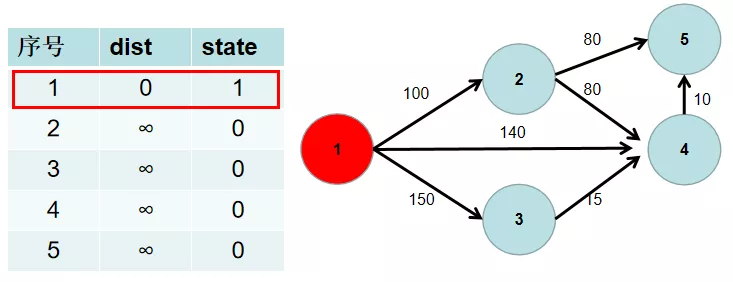
$Step\ 1$ 用一个 dist 数组保存源点到其余各个节点的距离，dist[i] 表示源点到节点 $i$ 的距离。初始时，dist 数组的各个元素为无穷大。用一个状态数组 state 记录是否找到了源点到该节点的最短距离，state[i] 如果为真，则表示找到了源点到节点 $i$ 的最短距离，state[i] 如果为假，则表示源点到节点 $i$ 的最短距离还没有找到。初始时，state 各个元素为假。

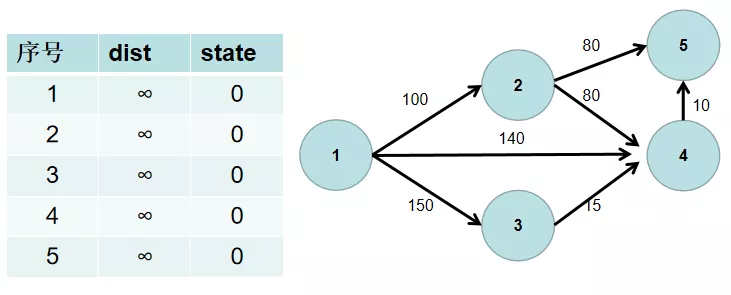
$Step\ 2$ 源点到源点的距离为 $0$。即dist[1] = 0。

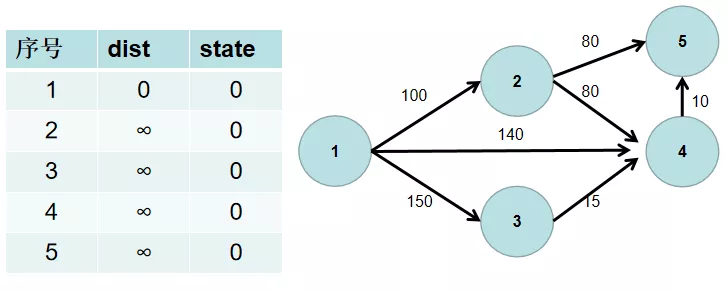
$Step\ 3$ 遍历 dist 数组，找到一个节点，这个节点是：没有确定最短路径的节点中距离源点最近的点。假设该节点编号为 $i$。此时就找到了源点到该节点的最短距离，state[i] 置为 $1$。

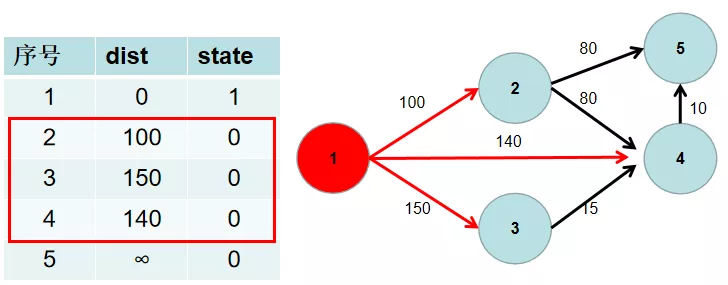
$Step\ 4$ 遍历 $i$ 所有可以到达的节点 $j$，如果 dist[j] 大于 dist[i] 加上 $i \to j$ 的距离，即 dist[j] > dist[i] + w[i][j]（w[i][j] 为 $i \to j$ 的距离），则更新 dist[j] = dist[i] + w[i][j]。 

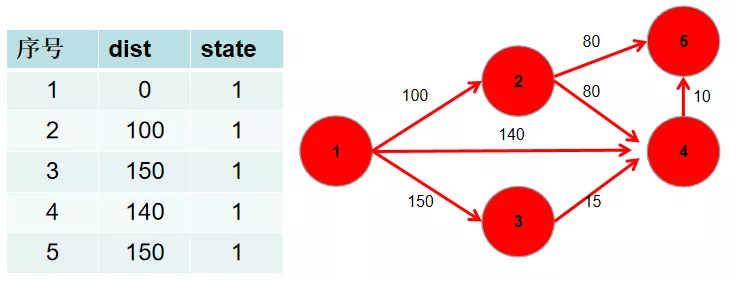
$Step\ 5$ 重复 $3\ 4$ 步骤，直到所有节点的状态都被置为 $1$。
$Step\ 6$ 此时 dist 数组中，就保存了源点到其余各个节点的最短距离。

【伪代码】

int dist[n],state[n];
dist[1] = 0, state[1] = 1;
for(i:1 ~ n) {
    t <- 没有确定最短路径的节点中距离源点最近的点;
    state[t] = 1;
    更新 dist;
}

【时间复杂度】
$O(n^2)$。
【代码细节】
必须数据

const LL INF=0x3f3f3f3f3f3f3f3f;
//顶点相关定义
const int N = 5e2+10;
bool state[N];//state 记录是否找到了源点到该节点的最短距离
LL dist[N];//dist 数组保存源点到其余各个节点的距离
LL h[N];
//边相关定义
const in M = 2e5+10;
LL e[M], ne[M], w[M], idx;//邻接矩阵存储图

LL n, m;//图的节点个数和边数

初始化

memset(h, -1, sizeof(h));//邻接矩阵初始化

加边

void add(int a, int b, int c) {//插入边 a->b 权值为 c
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx++;
}

朴素版算法实现

void Dijkstra() {
    memset(dist, 0x3f, sizeof(dist));//dist 数组的各个元素为无穷大
    memset(state, false, sizeof(state));
 
    dist[1] = 0;//源点到源点的距离为置为 0
    for (LL i = 0; i < n; i++) {
        LL t = -1;
        for (LL j = 1; j <= n; j++)//遍历 dist 数组，找到没有确定最短路径的节点中距离源点最近的点t
        {
            if (!state[j] && (t == -1 || dist[j] < dist[t]))
                t = j;
        }

        state[t] = 1;//state[i] 置为 1。

        for (LL j = h[t]; j != -1; j = ne[j])//遍历 t 所有可以到达的节点 i
        {
            LL i = e[j];
            dist[i] = min(dist[i], dist[t] + w[j]);//更新 dist[j]
        }
    }
}

【优化版】
我们可以使用小顶堆来优化，这样算法的时间复杂读度变为 $O(n+mlogn)$。

LL dijkstra() {
   memset(dist, 0x3f, sizeof dist);//距离初始化为无穷大
   memset(vis, false, sizeof vis);

    dist[1] = 0;
    priority_queue<PLL, vector<PLL>, greater<PLL>> heap;//小根堆
    heap.push({0, 1});//插入距离和节点编号

    while (heap.size())    {
        auto t = heap.top();//取距离源点最近的点
        heap.pop();

        LL ver = t.second, distance = t.first;//ver:节点编号，distance:源点距离ver 的距离

        if (vis[ver]) continue;//如果距离已经确定，则跳过该点
        vis[ver] = true;

        for (int i = h[ver]; i != -1; i = ne[i])//更新ver所指向的节点距离
        {
            LL j = e[i];
            if (dist[j] > dist[ver] + w[i]) {
                dist[j] = dist[ver] + w[i];
                heap.push({dist[j], j});//距离变小，则入堆
            }
        }
    }

    if (dist[n] == INF) return -1;
    return dist[n];
}