【Prim】

Prim 算法干的事情是：给定一个无向图，在图中选择若干条边把图的所有节点连起来。要求边长之和最小。在图论中，叫做求最小生成树。
Prim 算法采用的是一种贪心的策略。
每次将离连通部分的最近的点和点对应的边加入的连通部分，连通部分逐渐扩大，最后将整个图连通起来，并且边长之和最小。
Prim 算法复杂度与图的顶点 $n$ 的数量有关，和图的边数 $m$ 无关。一般 Prim 算法都是针对稠密图。

【步骤】

我们将图中各个节点用数字 $1 \sim n$ 编号。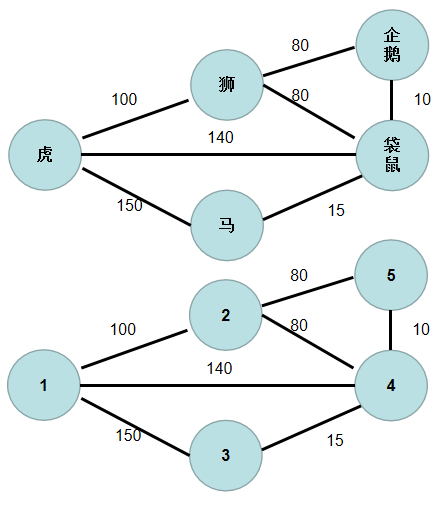

要将所有景点连通起来，并且边长之和最小。步骤如下：
$Step\ 1$. 用一个 state 数组表示节点是否已经连通。state[i] 为真，表示已经连通，state[i] 为假，表示还没有连通。初始时，state 各个元素为假。即所有点还没有连通。
用一个 dist 数组保存各个点到连通部分的最短距离，dist[i] 表示 $i$ 节点到连通部分的最短距离。初始时，dist 数组的各个元素为无穷大。
用一个 pre 数组保存节点的是和谁连通的。pre[i] = k 表示节点 $i$ 和节点 $k$ 之间需要有一条边。初始时，pre 的各个元素置为 $-1$。

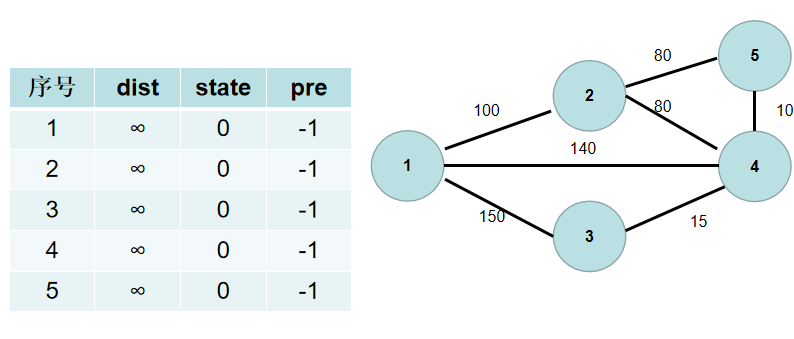
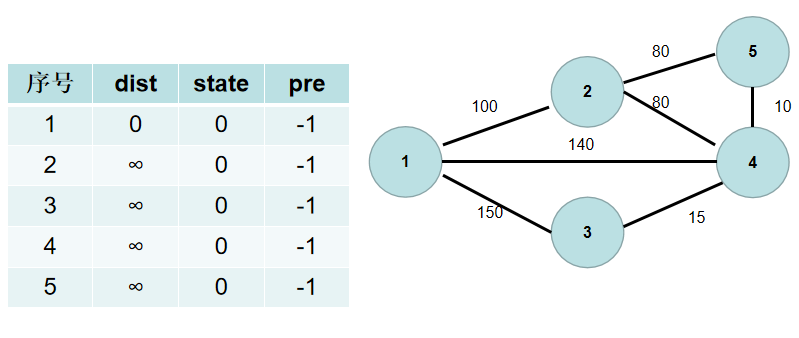
$Step\ 2$. 从 $1$ 号节点开始扩充连通的部分，所以 $1$ 号节点与连通部分的最短距离为 $0$，即 disti[1] 置为 $0$。

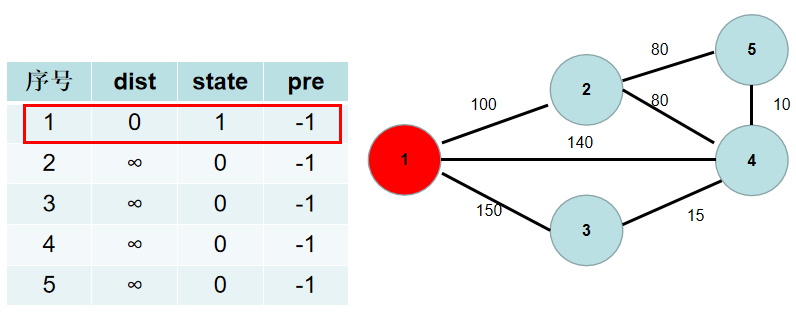
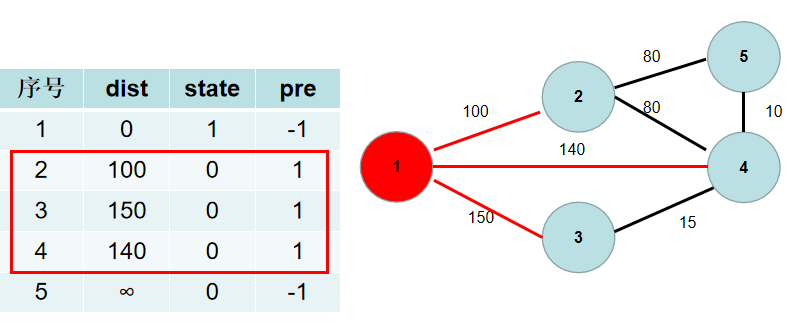
$Step\ 3$. 遍历 dist 数组，找到一个还没有连通起来，但是距离连通部分最近的点，假设该节点的编号是 $i$。$i$ 节点就是下一个应该加入连通部分的节点，stata[i] 置为 $1$。
用青色点表示还没有连通起来的点，红色点表示连通起来的点。这里青色点中距离最小的是 dist[1]，因此 state[1] 置为 $1$。

$Step\ 4$. 遍历所有与 $i$ 相连但没有加入到连通部分的点 $j$，如果 $j$ 距离连通部分的距离大于 $i\ j$ 之间的距离，即 dist[j] > w[i][j]（w[i][j] 为 $i\ j$ 节点之间的距离），则更新 dist[j] 为 w[i][j]。这时候表示，$j$ 到连通部分的最短方式是和 i 相连，因此，更新pre[j] = i。
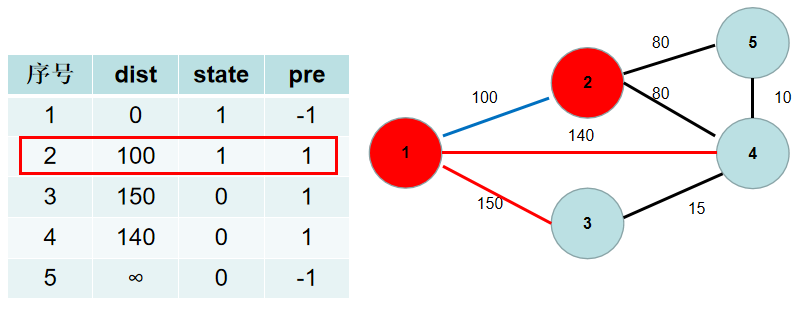
与节点 $1$ 相连的有 $2, 3, 4$ 号节点。$1 \to 2$ 的距离为 $100$，小于 dist[2]，dist[2] 更新为 $100$，pre[2] 更新为 $1$。$1 \to 4$ 的距离为 $140$，小于 dist[4]，dist[4] 更新为 $140$，pre[2] 更新为 $1$。$1 \to 3$ 的距离为 $150$，小于 dist[3]，dist[3] 更新为 $150$，pre[3] 更新为 $1$。

$Step\ 5$. 重复 Step 3 4 步骤，直到所有节点的状态都被置为 $1$。这里青色点中距离最小的是 dist[2]，因此 state[2] 置为 $1$。

与节点 $2$ 相连的有 $5, 4$ 号节点。$2 \to 5$ 的距离为 $80$，小于 dist[5]，dist[5] 更新为 $80$，pre[5] 更新为 $2$。$2 \to 4$ 的距离为 $80$，小于 dist[4]，dist[4] 更新为 $80$，pre[4] 更新为 $2$。

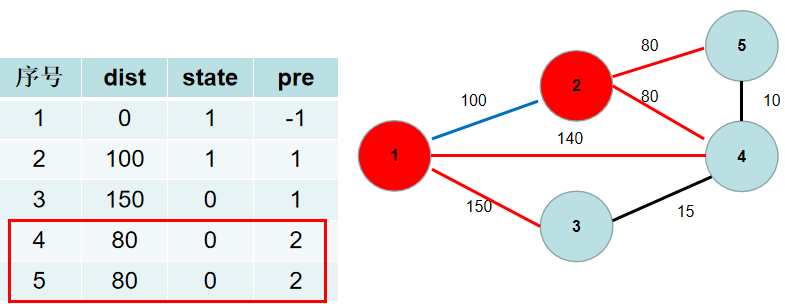
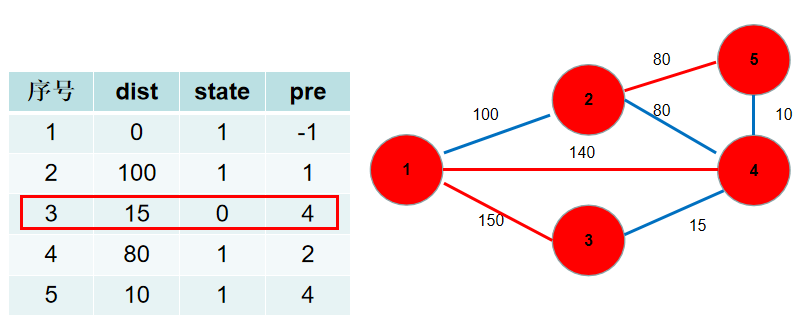
选 dist[4]，更新 dist[3]，dist[5]，pre[3]，pre[5]。


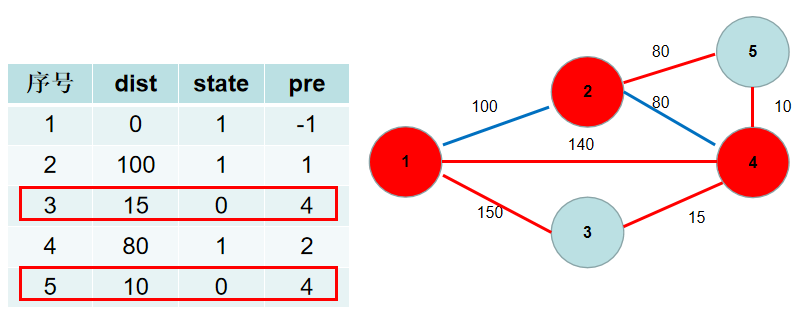
选 dist[5]，没有可更新的。


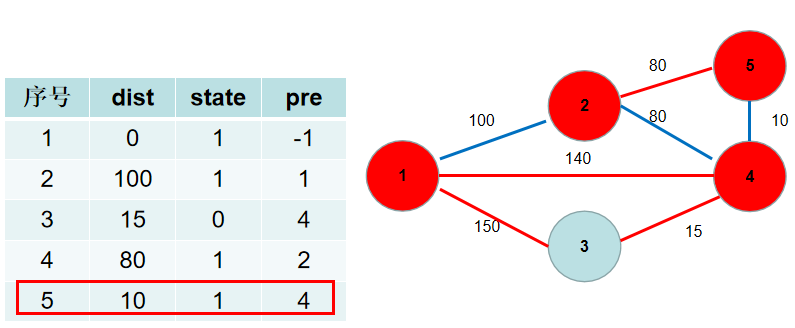
选 dist[3]，没有可更新的。

$Step\ 6$. 此时 dist 数组中保存了各个节点需要修的路长，加起来就是。pre 数组中保存了需要选择的边。

对应的伪代码为

int dist[n],state[n],pre[n];
dist[1] = 0;
for(i : 1 ~ n)
{
    t <- 没有连通起来，但是距离连通部分最近的点;
    state[t] = 1;
    更新 dist 和 pre;
}

【时间复杂度】

$O(n^2)$。
【代码】
必须数据

const LL INF = 0x3f3f3f3f3f3f3f3f;
const int N = 1e3+10;
bool vis[N];//可见性控制
LL g[N][N];//存储图
LL dis[N];//存储各个节点到生成树的距离
LL st[N];//节点是否被加入到生成树中
LL pre[N];//节点的前去节点
LL n, m;//n 个节点，m 条边

初始化

memset(g, 0x3f, sizeof(g));//各个点之间的距离初始化成很大的数 INF
memset(dis, 0x3f, sizeof dis);//各个点之间的距离初始化成很大的数 INF
memset(vis, false, sizeof vis);

数据读取

    cin >> n >> m;//输入节点数和边数
    while(m --)
    {
        int a, b, w;
        cin >> a >> b >> w;//输出边的两个顶点和权重
        g[a] = g[a] = min(g[a],w);//存储权重
    }

Prim 算法实现

int prim()
{
    memset(dt,0x3f, sizeof(dt));//初始化距离数组为一个很大的数（10亿左右）
    int res= 0;
    dt[1] = 0;//从 1 号节点开始生成 
    for(int i = 1; i <= n; i++)//每次循环选出一个点加入到生成树
    {
        int id = -1;
        for(int j = 1; j <= n; j++)//每个节点一次判断
        {
            if(!st[j] && (id == -1 || dt[j] < dt[id]))//如果没有在树中，且到树的距离最短，则选择该点
                id = j;
        }

        st[id] = true;// 选择该点
        res += dt[id];
        for(int i = 1; i <= n; i++)//更新生成树外的点到生成树的距离
        {
            if(dt[i] > g[id][i] && !st[i])//从 t 到节点 i 的距离小于原来距离，则更新。
            {
                dt[i] = g[id][i];//更新距离
                pre[i] = id;//从 id 到 i 的距离更短，i 的前驱变为 id.
            }
        }
    }
    return res;
}

最小生成树路径

void getPath()//输出各个边
{
    for(int i = n; i > 1; i--)//n 个节点，所以有 n-1 条边。
    {
        cout << i <<" " << pre[i] << " "<< endl;// i 是节点编号，pre[i] 是 i 节点的前驱节点。他们构成一条边。
    }
}