Consider two points,  $p=(p_x, p_y)$ and $q=(q_x, q_y)$. We consider the inversion or point reflection, $r=(r_x, r_y)$ of point $p$ across point $q$ to be a $180^°$ rotation of point $p$ around $q$.
Given  $n$ sets of points $p$ and $q$, find $r$ for each pair of points and print two space-separated integers denoting the respective values of $r_x$ and $r_y$ on a new line.

The first line contains an integer, $n\ (1 \leq n \leq 1,000)$ denoting the number of sets of points.
Each of the $n$ subsequent lines contains four space-separated integers that describe the respective values of $p_x, p_y, q_x, q_y$  defining points $p$ and $q$.

Each of the $n$ subsequent lines contains two space-separated integers that $x$ and $y$ coordinates of the reflected point $r$.

$1 \leq n \leq 1,000\\
-10^9 \leq p_x,p_y,q_x,q_y \leq 10^9$

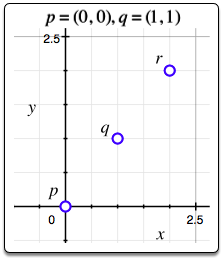
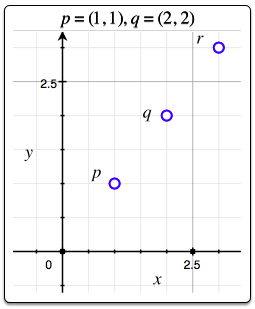
2 2
3 3

The graphs below depict points $p,q ,r$ for the $n=2$ points given as Sample Input.
Sample $1$

Sample $2$